Resistors are fundamental components in electronic circuits, controlling current flow and voltage levels. Whether you’re designing a simple LED circuit or a complex audio amplifier, understanding resistor calculations is essential for successful electronics projects. This comprehensive guide covers everything you need to know about resistors, from color codes to series and parallel configurations, providing you with the knowledge to make accurate calculations for your electronic designs.
What Are Resistors and Why Are They Important?

Different types of resistors used in electronic circuits
Resistors are passive two-terminal electrical components that implement electrical resistance in electronic circuits. They limit current flow, adjust signal levels, divide voltages, bias active elements, and terminate transmission lines among other uses.
The resistance value is measured in ohms (Ω) and determines how much the resistor opposes the flow of electric current. Higher resistance values mean less current flows through the component at a given voltage.
Key Functions of Resistors in Circuits
- Limiting current to protect sensitive components
- Creating voltage dividers for signal processing
- Establishing bias points in amplifier circuits
- Controlling timing in RC (resistor-capacitor) circuits
- Providing feedback in operational amplifier circuits
Common Resistor Applications
- LED current limiting to prevent burnout
- Pull-up and pull-down resistors in digital circuits
- Volume controls and tone adjustments in audio equipment
- Voltage sensing in measurement circuits
- Power dissipation in heating elements
Need Precise Resistor Calculations?
Stop guessing resistor values and get accurate results instantly with our easy-to-use calculator.
Types of Resistors and Their Applications

Carbon Film Resistors
Carbon film resistors are made by depositing a thin carbon film on a ceramic substrate. They’re inexpensive and suitable for general-purpose applications.
Tolerance: Typically 5-10%
Best for: General electronics, non-critical applications
Metal Film Resistors
Metal film resistors offer better precision and stability than carbon film. They have lower noise and are more reliable over time and temperature changes.
Tolerance: 0.1-2%
Best for: Audio equipment, precision measurement circuits
Wirewound Resistors
Wirewound resistors consist of metal wire wrapped around a ceramic core. They can handle high power and provide excellent stability.
Tolerance: 0.01-1%
Best for: Power supplies, high-current applications
SMD Resistors
Surface Mount Device (SMD) resistors are tiny components designed for automated assembly on printed circuit boards.
Tolerance: 0.1-5%
Best for: Modern electronics, space-constrained applications
Variable Resistors
Variable resistors (potentiometers) allow resistance adjustment, making them ideal for volume controls and calibration circuits.
Tolerance: 5-20%
Best for: Control applications, adjustable settings
Thermistors
Thermistors change resistance with temperature, making them useful for temperature sensing and compensation.
Types: NTC (negative temperature coefficient) and PTC (positive temperature coefficient)
Best for: Temperature measurement, thermal protection
Understanding Resistor Color Codes
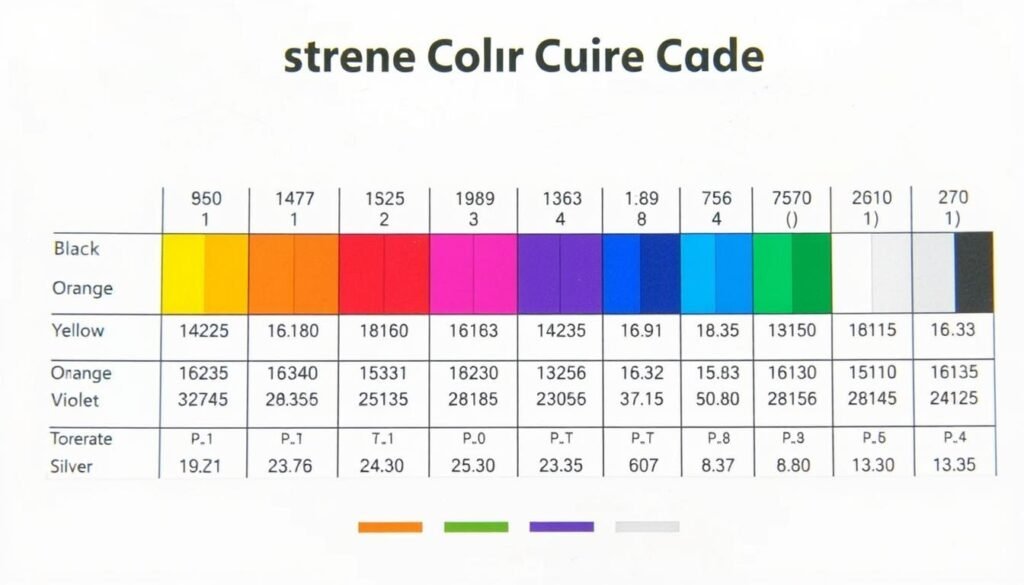
Resistor color codes are a standardized way to indicate resistance values and tolerance on small components where printing numbers would be impractical. Understanding how to read these color bands is essential for electronics work.
How to Read 4-Band Resistors
The most common resistors have four color bands:
- 1st Band: First significant digit
- 2nd Band: Second significant digit
- 3rd Band: Multiplier (power of 10)
- 4th Band: Tolerance

5-Band and 6-Band Resistors
Precision resistors often use 5 or 6 bands for greater accuracy:
5-Band Resistors:
- 1st Band: First significant digit
- 2nd Band: Second significant digit
- 3rd Band: Third significant digit
- 4th Band: Multiplier
- 5th Band: Tolerance
6-Band Resistors:
- 1st-5th Bands: Same as 5-band resistors
- 6th Band: Temperature coefficient (ppm/°C)
| Color | 1st-3rd Bands (Digit) | Multiplier | Tolerance | Temp. Coefficient |
| Black | 0 | ×1 | – | 250 ppm/K |
| Brown | 1 | ×10 | ±1% | 100 ppm/K |
| Red | 2 | ×100 | ±2% | 50 ppm/K |
| Orange | 3 | ×1K | ±0.05% | 15 ppm/K |
| Yellow | 4 | ×10K | ±0.02% | 25 ppm/K |
| Green | 5 | ×100K | ±0.5% | 20 ppm/K |
| Blue | 6 | ×1M | ±0.25% | 10 ppm/K |
| Violet | 7 | ×10M | ±0.1% | 5 ppm/K |
| Gray | 8 | ×100M | ±0.01% | 1 ppm/K |
| White | 9 | ×1G | – | – |
| Gold | – | ×0.1 | ±5% | – |
| Silver | – | ×0.01 | ±10% | – |
| None | – | – | ±20% | – |
Example Color Code Calculations
Example 1: 4-Band Resistor
Colors: Red, Violet, Orange, Gold
Calculation:
- Red (2) = 1st digit
- Violet (7) = 2nd digit
- Orange (×1,000) = Multiplier
- Gold (±5%) = Tolerance
Value: 27,000Ω or 27kΩ ±5%
Example 2: 5-Band Resistor
Colors: Brown, Black, Black, Red, Brown
Calculation:
- Brown (1) = 1st digit
- Black (0) = 2nd digit
- Black (0) = 3rd digit
- Red (×100) = Multiplier
- Brown (±1%) = Tolerance
Value: 10,000Ω or 10kΩ ±1%
Example 3: 6-Band Resistor
Colors: Blue, Gray, Green, Brown, Brown, Red
Calculation:
- Blue (6) = 1st digit
- Gray (8) = 2nd digit
- Green (5) = 3rd digit
- Brown (×10) = Multiplier
- Brown (±1%) = Tolerance
- Red (50 ppm/K) = Temp. coefficient
Value: 6,850Ω or 6.85kΩ ±1%, 50 ppm/K
Decode Resistor Color Bands Instantly
No more manual calculations or referencing color code charts. Our calculator does the work for you!
Series and Parallel Resistor Configurations
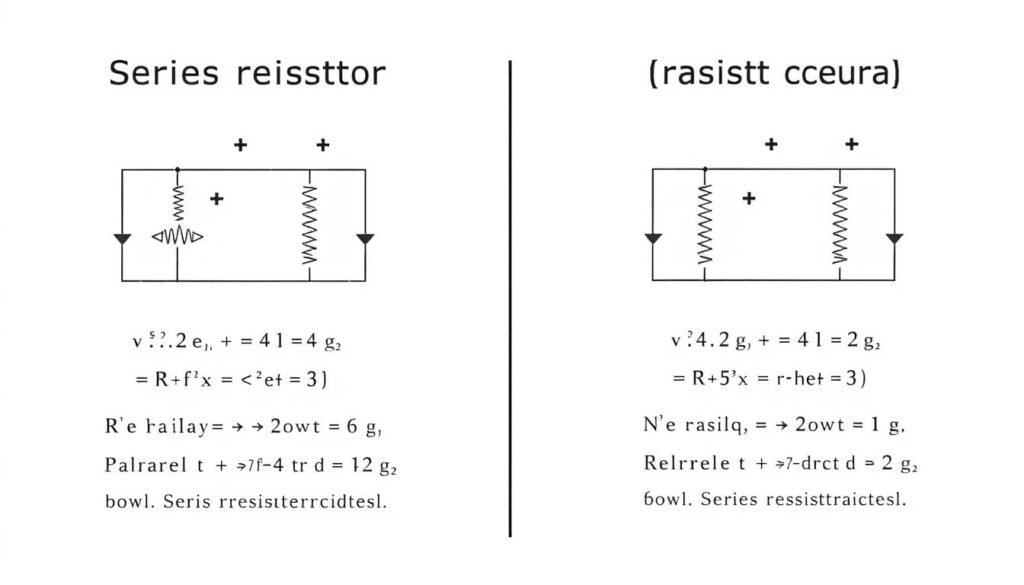
Understanding how to calculate total resistance when resistors are connected in series or parallel is fundamental to circuit design. Each configuration has different properties and applications in electronic circuits.
Resistors in Series
When resistors are connected end-to-end, they form a series circuit. In this configuration, the same current flows through each resistor, but the voltage is divided among them.
Series Resistance Formula:
Rtotal = R1 + R2 + R3 + … + Rn
Example Calculation:
For resistors of 100Ω, 220Ω, and 330Ω in series:
Rtotal = 100Ω + 220Ω + 330Ω = 650Ω
Applications of Series Resistors:
- Voltage dividers
- Current limiting
- Level shifting
- Creating specific resistance values
Resistors in Parallel
When resistors are connected across the same two points, they form a parallel circuit. In this configuration, the voltage across each resistor is the same, but the current divides among them.
Parallel Resistance Formula:
1/Rtotal = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
For two resistors: Rtotal = (R1 × R2) / (R1 + R2)
Example Calculation:
For resistors of 100Ω and 100Ω in parallel:
Rtotal = (100Ω × 100Ω) / (100Ω + 100Ω) = 10,000Ω / 200Ω = 50Ω
Applications of Parallel Resistors:
- Current division
- Creating lower resistance values
- Increasing power handling capability
- Providing alternative current paths
Series-Parallel Combinations
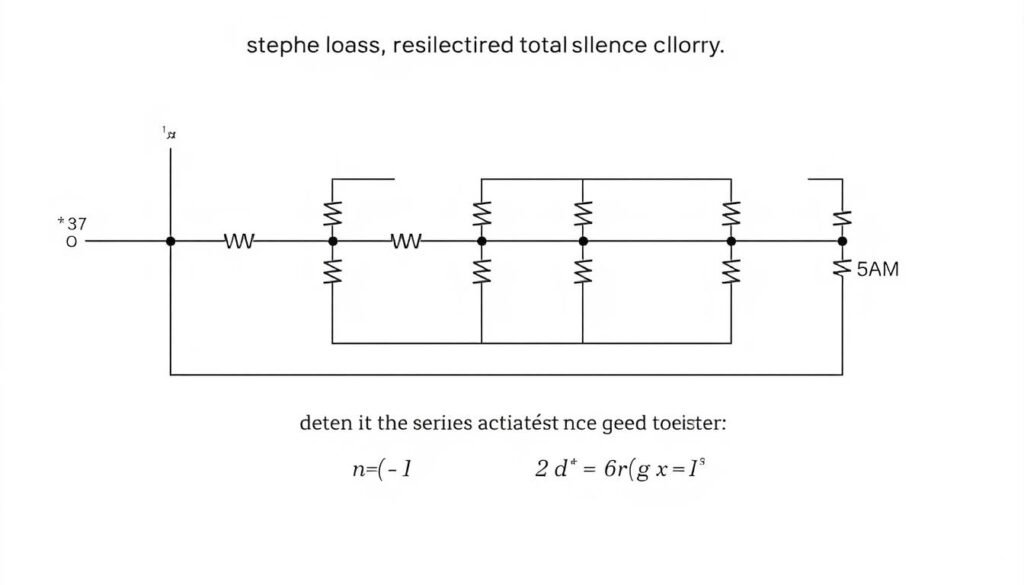
Many practical circuits contain combinations of series and parallel resistors. To calculate the total resistance, break down the circuit into simpler series and parallel sections, then combine them step by step.
Calculation Tip: When analyzing complex resistor networks, start by identifying the innermost series or parallel groups, calculate their equivalent resistance, and then work outward.
Example of Series-Parallel Calculation:
Consider a circuit with R1 = 100Ω and R2 = 200Ω in series, and this combination is in parallel with R3 = 300Ω.
- Calculate the series combination: R1 + R2 = 100Ω + 200Ω = 300Ω
- Calculate the parallel combination: (300Ω × 300Ω) / (300Ω + 300Ω) = 90,000Ω / 600Ω = 150Ω
- Total resistance = 150Ω
Standard Resistor Values and Tolerance Series
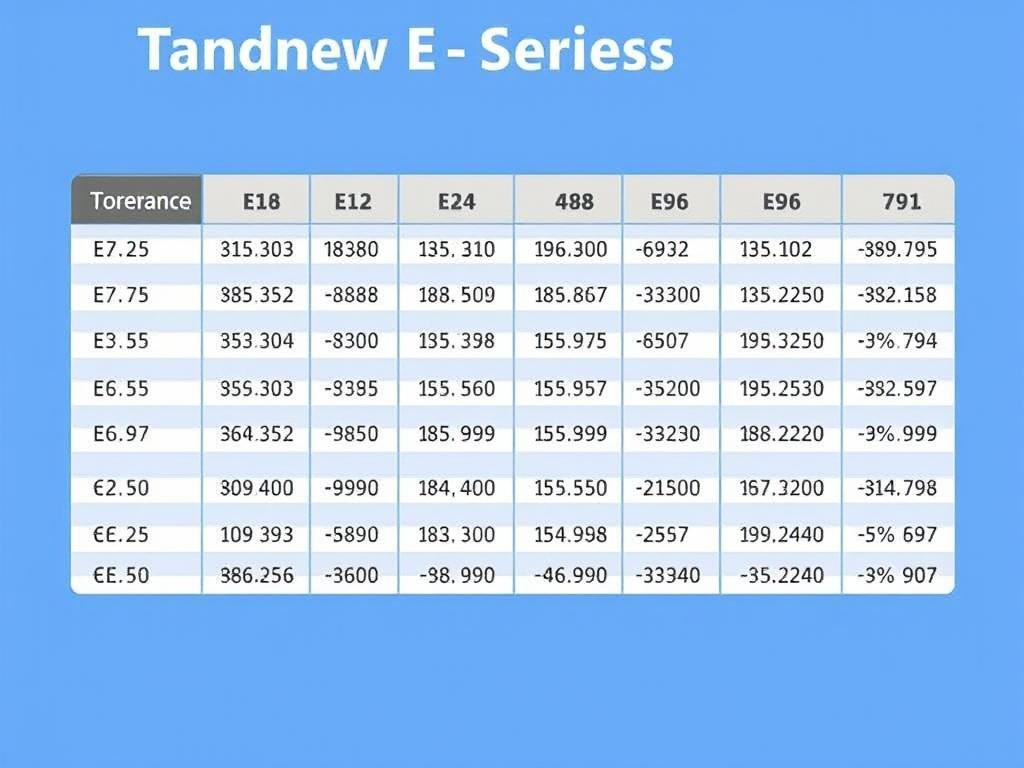
Resistors are manufactured in standardized values according to internationally recognized series. These series, designated as E6, E12, E24, E48, E96, and E192, indicate the number of values available per decade and correspond to specific tolerance levels.
| Series | Tolerance | Values per Decade | Example Values (First Decade) |
| E6 | ±20% | 6 | 10, 15, 22, 33, 47, 68 |
| E12 | ±10% | 12 | 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82 |
| E24 | ±5% | 24 | 10, 11, 12, 13, 15, 16, 18, 20, 22, 24, 27, 30, 33, 36, 39, 43, 47, 51, 56, 62, 68, 75, 82, 91 |
| E48 | ±2% | 48 | 10.0, 10.5, 11.0, 11.5, 12.1, 12.7, 13.3, 14.0, 14.7, 15.4, 16.2, 16.9, 17.8, 18.7, 19.6, 20.5… |
| E96 | ±1% | 96 | 10.0, 10.2, 10.5, 10.7, 11.0, 11.3, 11.5, 11.8, 12.1, 12.4, 12.7, 13.0… |
| E192 | ±0.5%, ±0.25%, ±0.1% | 192 | 10.0, 10.1, 10.2, 10.4, 10.5, 10.6, 10.7, 10.9, 11.0, 11.1, 11.3… |
Why Standard Values Matter
Understanding standard resistor values is crucial when designing circuits because:
- You’ll need to select from available values rather than theoretical ones
- Higher precision (lower tolerance) resistors come in more values but cost more
- Combining standard values in series or parallel can achieve non-standard values
- Circuit designs often need to account for component tolerances
Find the Perfect Resistor Value
Our calculator helps you identify the closest standard resistor value for your circuit design needs.
Practical Applications and Troubleshooting

Common Applications of Resistor Calculations
LED Current Limiting
LEDs require resistors to limit current and prevent damage. The formula to calculate the appropriate resistor value is:
R = (Vsupply – VLED) / ILED
Where Vsupply is the source voltage, VLED is the LED forward voltage, and ILED is the desired LED current.
Voltage Dividers
Voltage dividers use two resistors to create a specific output voltage from a higher input voltage:
Vout = Vin × (R2 / (R1 + R2))
This is commonly used in sensor circuits, reference voltages, and biasing networks.
Pull-up/Pull-down Resistors
These resistors establish a default logic state in digital circuits when inputs are floating:
- Pull-up: Connects to positive supply
- Pull-down: Connects to ground
Typical values range from 1kΩ to 100kΩ depending on the application.
Troubleshooting Resistor Issues

Common Resistor Problems
- Incorrect Resistance: Using wrong value or misreading color code
- Tolerance Issues: Component variation exceeding circuit requirements
- Power Rating: Resistor overheating due to insufficient wattage rating
- Open Circuit: Resistor burned out or physically damaged
- Noise: Carbon composition resistors generating excess noise
Diagnostic Techniques
- Multimeter Testing: Measure resistance directly (disconnect from circuit first)
- Visual Inspection: Look for burn marks, discoloration, or physical damage
- Voltage Drop Testing: Measure voltage across resistor in circuit
- Thermal Imaging: Identify overheating resistors
- Substitution: Replace suspect resistor with known good component
Safety Note: Always disconnect power before measuring resistors in-circuit. High-wattage resistors can become extremely hot during operation and cause burns if touched.
Frequently Asked Questions About Resistors
How do I determine the power rating needed for a resistor?
Calculate the power using P = V² / R or P = I² × R, where P is power in watts, V is voltage across the resistor, I is current through the resistor, and R is resistance. Choose a resistor with a power rating at least twice the calculated value for safety margin.
What happens if I use a resistor with the wrong tolerance?
Using a resistor with wider tolerance than required (e.g., ±5% instead of ±1%) may cause circuit performance to vary more than designed. In precision applications like voltage references or filters, this can lead to significant errors. In non-critical applications like LED current limiting, wider tolerances are often acceptable.
How do I read SMD (Surface Mount Device) resistor codes?
SMD resistors use numerical codes instead of color bands. For three-digit codes, the first two digits are significant figures and the third is the multiplier (number of zeros). For example, “103” means 10 followed by 3 zeros, or 10,000Ω (10kΩ). Four-digit codes include a tolerance indicator.
Can I replace a resistor with one of a slightly different value?
It depends on the circuit’s sensitivity. In non-critical applications, values within 10-20% of the original may work fine. For precision circuits, stay within the original tolerance. Always ensure the replacement has an adequate power rating. When in doubt, use the exact specified value.
Why is my measured resistance different from the color code value?
Several factors can cause this:
- The resistor is within its tolerance range (e.g., a 1kΩ ±5% resistor can measure between 950Ω and 1050Ω)
- Temperature effects (resistance changes with temperature)
- Measurement errors (probe resistance, meter calibration)
- Resistor damage or aging
If the measurement is within the tolerance range, the resistor is likely functioning correctly.
Ready to Simplify Your Resistor Calculations?
Our Resistor Calculator handles color codes, series/parallel configurations, and standard values – all in one easy-to-use tool.
Conclusion
Understanding resistor calculations is fundamental to successful electronics design. From interpreting color codes to calculating series and parallel combinations, these skills form the foundation of circuit analysis and troubleshooting. Whether you’re a student, hobbyist, or professional engineer, having a reliable resistor calculator at your disposal can save time and prevent errors in your projects.
Our comprehensive Resistor Calculator tool provides instant, accurate results for all your resistor-related calculations. It eliminates the guesswork from reading color codes, finding standard values, and determining series and parallel combinations. With this knowledge and the right tools, you’ll be well-equipped to tackle any electronic circuit design challenge.
Explore Our Complete Suite of Electronics Calculators
From resistors to capacitors, Ohm’s Law to LED current limiting – we have all the calculation tools you need for your electronics projects.