Percentages are everywhere in our daily lives – from calculating discounts while shopping to determining grades on exams, figuring out tips at restaurants, or understanding interest rates on loans. A percentage calculator makes these calculations quick and error-free, saving you time and helping you make better decisions. In this comprehensive guide, we’ll explore what percentages are, how to calculate them, and provide step-by-step instructions for solving various percentage problems.
What is a Percentage?
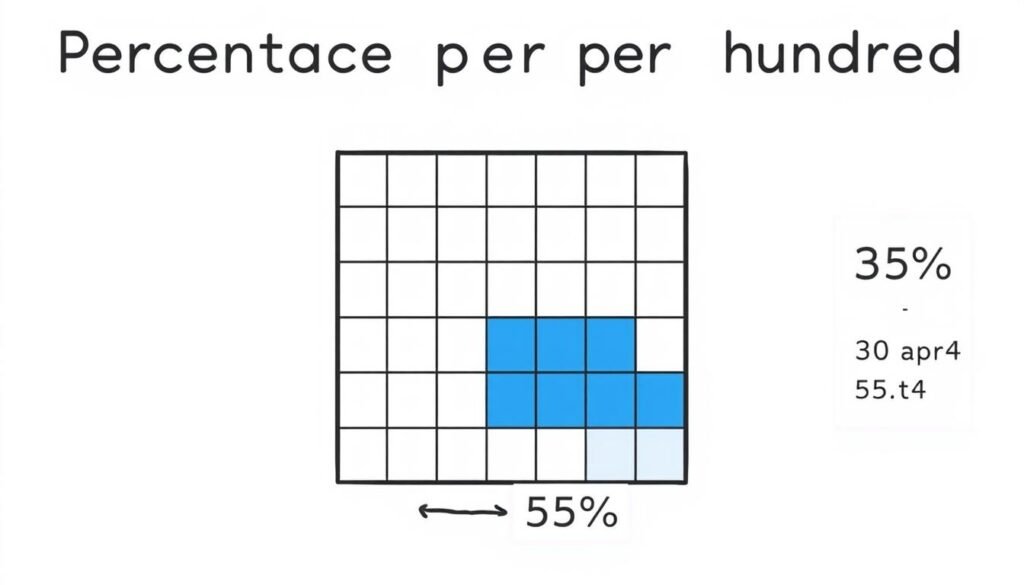
Percentages represent parts per hundred
A percentage is a way to express a number as a fraction of 100. The word “percentage” comes from the Latin “per centum,” meaning “by the hundred.” Percentages are denoted by the symbol “%”. For example, 50% means 50 out of 100, or half of the whole.
Percentages provide a standardized way to compare values, express proportions, and calculate changes. They’re especially useful when dealing with different scales or when you need to understand relative amounts rather than absolute values.
Converting Between Percentages, Decimals, and Fractions
| Conversion Type | Formula | Example |
| Decimal to Percentage | Multiply by 100 and add % symbol | 0.75 = 75% |
| Percentage to Decimal | Remove % symbol and divide by 100 | 25% = 0.25 |
| Fraction to Percentage | Divide numerator by denominator, multiply by 100 | 3/4 = 0.75 = 75% |
| Percentage to Fraction | Remove % symbol, put over 100, simplify | 20% = 20/100 = 1/5 |
The Percentage Formula: Understanding the Basics

The basic percentage formula can be written in several ways depending on what you’re trying to calculate. Here are the three fundamental percentage formulas:
Finding the Percentage
P% = (X/Y) × 100
This formula helps you find what percent one number is of another.
Example: What percent of 50 is 10?
P% = (10/50) × 100 = 20%
Finding the Part
X = (P% × Y) / 100
This formula helps you find a percentage of a given number.
Example: What is 15% of 80?
X = (15 × 80) / 100 = 12
Finding the Whole
Y = (X × 100) / P%
This formula helps you find the total when you know a part and its percentage.
Example: 24 is 30% of what number?
Y = (24 × 100) / 30 = 80
Common Percentage Calculations
Let’s explore some of the most common percentage calculations you might need in everyday life.
How to Calculate a Percentage of a Number

To find a percentage of a number, convert the percentage to a decimal and multiply:
- Convert the percentage to a decimal by dividing by 100
- Multiply the decimal by the number
Example: Calculate 35% of $200
- Convert 35% to a decimal: 35 ÷ 100 = 0.35
- Multiply: 0.35 × $200 = $70
- Therefore, 35% of $200 is $70
How to Find What Percent One Number is of Another
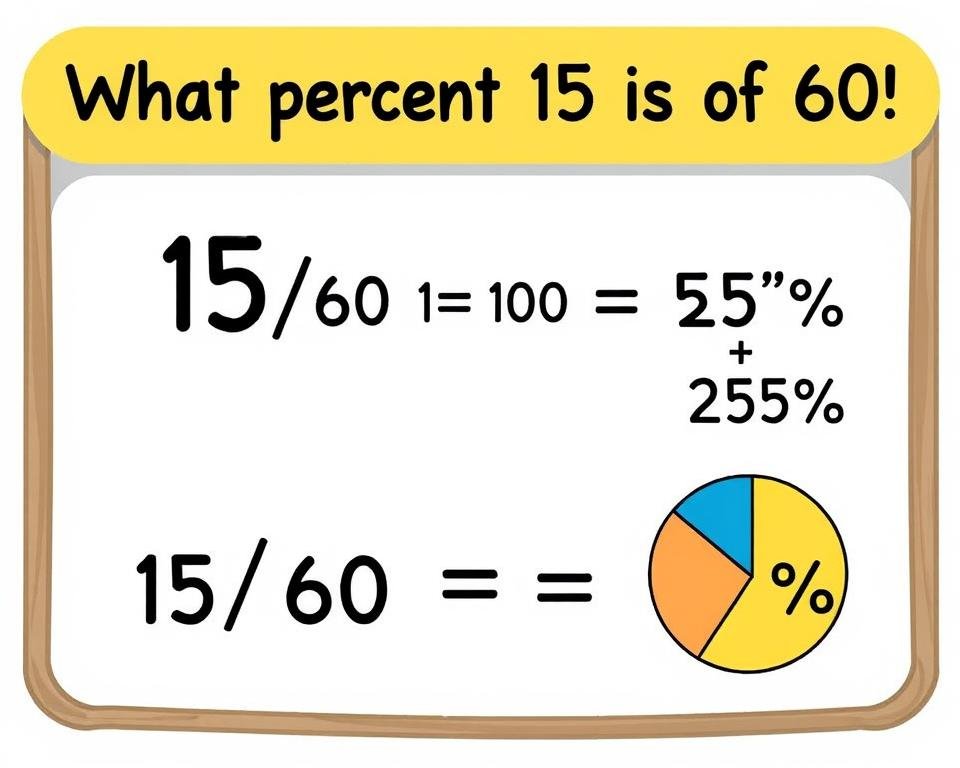
To find what percent one number is of another:
- Divide the first number by the second number
- Multiply the result by 100 and add the % symbol
Example: What percent of 80 is 20?
- Divide: 20 ÷ 80 = 0.25
- Multiply by 100: 0.25 × 100 = 25%
- Therefore, 20 is 25% of 80
Calculating Percentage Increase and Decrease

Percentage Increase Formula
To calculate percentage increase:
Percentage Increase = ((New Value – Original Value) / Original Value) × 100
Example: A shirt’s price increased from $40 to $50. What is the percentage increase?
- Calculate the increase: $50 – $40 = $10
- Divide by the original value: $10 ÷ $40 = 0.25
- Multiply by 100: 0.25 × 100 = 25%
- Therefore, the price increased by 25%
Percentage Decrease Formula
To calculate percentage decrease:
Percentage Decrease = ((Original Value – New Value) / Original Value) × 100
Example: A car’s value depreciated from $20,000 to $15,000. What is the percentage decrease?
- Calculate the decrease: $20,000 – $15,000 = $5,000
- Divide by the original value: $5,000 ÷ $20,000 = 0.25
- Multiply by 100: 0.25 × 100 = 25%
- Therefore, the car’s value decreased by 25%
Understanding Percentage Difference

Percentage difference measures the relative difference between two values when neither is considered a reference or original value. This is useful when comparing two independent values.
Percentage Difference = (|Value1 – Value2| / ((Value1 + Value2) / 2)) × 100
Example: Compare the populations of two cities: City A has 150,000 residents and City B has 180,000 residents.
- Calculate the absolute difference: |150,000 – 180,000| = 30,000
- Calculate the average: (150,000 + 180,000) / 2 = 165,000
- Divide the difference by the average: 30,000 ÷ 165,000 = 0.1818
- Multiply by 100: 0.1818 × 100 = 18.18%
- Therefore, the percentage difference between the populations is 18.18%
Real-World Applications of Percentage Calculations
Shopping Discounts
When a store offers a 25% discount on a $80 item:
Discount amount = 25% of $80 = 0.25 × $80 = $20
Final price = $80 – $20 = $60
Tipping at Restaurants
For a 15% tip on a $45 bill:
Tip amount = 15% of $45 = 0.15 × $45 = $6.75
Total payment = $45 + $6.75 = $51.75
Academic Grades
If you scored 42 points out of 50 on a test:
Percentage = (42 ÷ 50) × 100 = 84%
This helps standardize scores across different tests.
Sales Tax Calculation
For an 8% sales tax on a $120 purchase:
Tax amount = 8% of $120 = 0.08 × $120 = $9.60
Total cost = $120 + $9.60 = $129.60
Interest Rates
A 5% annual interest rate on a $1,000 savings account:
Interest earned = 5% of $1,000 = 0.05 × $1,000 = $50 per year
Health and Nutrition
If a food label shows 12g of protein providing 24% of daily value:
100% daily value = (12g ÷ 24) × 100 = 50g of protein
Tips for Quick Percentage Calculations

Here are some mental math shortcuts to help you calculate percentages more quickly:
Finding Common Percentages
- 10%: Move the decimal point one place to the left (e.g., 10% of 250 = 25)
- 5%: Find 10% and divide by 2 (e.g., 5% of 250 = 12.5)
- 20%: Find 10% and multiply by 2 (e.g., 20% of 250 = 50)
- 25%: Divide by 4 (e.g., 25% of 250 = 62.5)
- 50%: Divide by 2 (e.g., 50% of 250 = 125)
Breaking Down Complex Percentages
- 15%: Find 10% and add half of that (e.g., 15% of 250 = 25 + 12.5 = 37.5)
- 33⅓%: Divide by 3 (e.g., 33⅓% of 250 = 83.33)
- 66⅔%: Multiply by 2/3 or find 33⅓% and double it (e.g., 66⅔% of 250 = 166.67)
- 75%: Find 50% and add half of that (e.g., 75% of 250 = 125 + 62.5 = 187.5)
Solving Common Percentage Problems

How do I calculate a percentage of a number?
To find a percentage of a number, convert the percentage to a decimal and multiply by the number.
Example: What is 40% of 75?
Step 1: Convert 40% to a decimal: 40 ÷ 100 = 0.4
Step 2: Multiply: 0.4 × 75 = 30
Therefore, 40% of 75 is 30.
How do I find what percent one number is of another?
To find what percent one number is of another, divide the first number by the second number and multiply by 100.
Example: 18 is what percent of 72?
Step 1: Divide: 18 ÷ 72 = 0.25
Step 2: Multiply by 100: 0.25 × 100 = 25%
Therefore, 18 is 25% of 72.
How do I find the original value when I know the percentage and the final value?
To find the original value when you know the percentage and the final value, divide the final value by the decimal equivalent of the percentage.
Example: After a 20% increase, the value is 240. What was the original value?
Step 1: Convert the percentage increase to a decimal and add 1: 1 + 0.2 = 1.2
Step 2: Divide the final value by this number: 240 ÷ 1.2 = 200
Therefore, the original value was 200.
How do I calculate percentage change?
To calculate percentage change, subtract the old value from the new value, divide by the old value, and multiply by 100.
Example: A product’s price changed from $80 to $92. What is the percentage change?
Step 1: Calculate the difference: $92 – $80 = $12
Step 2: Divide by the original value: $12 ÷ $80 = 0.15
Step 3: Multiply by 100: 0.15 × 100 = 15%
Therefore, the price increased by 15%.
Advanced Percentage Concepts
Percentage Points vs. Percentages
It’s important to distinguish between percentage points and percentages when discussing changes in percentages:
- Percentage points refer to the arithmetic difference between two percentages
- Percentage change refers to the relative change between two percentage values
Example: If an interest rate increases from 5% to 7%, we can describe this as:
- An increase of 2 percentage points (the arithmetic difference)
- A 40% increase (because 2% is 40% of 5%)
Compound Percentages
When multiple percentage changes are applied sequentially, the final result differs from simply adding the percentages together.
Example: If a $100 investment increases by 10% one year and then by 15% the next year:
- After first year: $100 × 1.10 = $110
- After second year: $110 × 1.15 = $126.50
- Total increase: $26.50 or 26.5% (not simply 10% + 15% = 25%)
Per Mille and Basis Points
For very small percentages, especially in finance, these alternative notations are used:
- Per mille (‰): One-tenth of a percent or one part per thousand
- Basis point (bp): One-hundredth of a percent or 0.01%
Example: An interest rate increase from 3.25% to 3.50% is an increase of 25 basis points.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is an essential skill that helps us make informed decisions in many aspects of life – from shopping and tipping to financial planning and academic assessment. By mastering the basic percentage formulas and practicing with real-world examples, you can become confident in handling any percentage calculation that comes your way.
While manual calculations are valuable for understanding the concepts, a percentage calculator can save you time and ensure accuracy, especially for complex calculations or when you need quick results.
Ready to Simplify Your Percentage Calculations?
Our Percentage Calculator makes it easy to find percentages, calculate increases and decreases, determine what percent one number is of another, and solve other percentage problems instantly – all without the risk of manual calculation errors.
Additional Resources for Percentage Calculations

Related Calculators
- Percentage Increase Calculator
- Percentage Decrease Calculator
- Percentage Difference Calculator
- Discount Calculator
- Tip Calculator
- Fraction to Percentage Converter
Learning Resources
- Percentage Practice Worksheets
- Video Tutorials on Percentage Calculations
- Interactive Percentage Games
- Step-by-Step Percentage Guides
- Real-World Percentage Problems
Advanced Topics
- Compound Interest Calculations
- Statistical Percentages and Probability
- Business Applications of Percentages
- Tax Calculation Strategies
- Financial Ratio Analysis
Need Help With Other Calculations?
Explore our full suite of calculators designed to help you solve math problems, financial questions, and everyday calculations quickly and accurately.