Use our free Rounding Calculator to quickly round numbers to any decimal place or whole number. Simple, accurate, and perfect for math, finance, and daily calculations.
Rounding numbers is a fundamental mathematical operation used to simplify values while maintaining an acceptable level of accuracy. Whether you’re working with financial calculations, scientific measurements, or everyday math, knowing how to properly round numbers is essential. Our Rounding Calculator makes this process effortless, allowing you to round any number to the nearest whole number, tenth, hundredth, or any other decimal place with perfect precision.
In this comprehensive guide, we’ll explore everything you need to know about rounding numbers, from basic rules to advanced techniques, real-world applications, and how our rounding calculator can save you time and eliminate errors.
Try Our Free Rounding Calculator
Round any number to your desired decimal place instantly. No registration required, completely free to use!
What is Rounding and Why is it Important?
Rounding is the process of replacing a number with an approximate value that has fewer significant digits while maintaining a similar magnitude. This mathematical technique helps simplify calculations, make numbers more manageable, and present data in a more digestible format.
Rounding is crucial in many fields:
- In finance, monetary values are typically rounded to the nearest cent
- In science, measurements are rounded based on the precision of measuring instruments
- In statistics, data points are often rounded to make trends more apparent
- In everyday life, we round prices, times, and quantities for convenience
Using a rounding calculator ensures accuracy and consistency in your rounded results, eliminating the potential for human error when applying rounding rules to complex numbers.
Basic Rules of Rounding Numbers
The standard rules for rounding numbers are straightforward but must be applied consistently to ensure accurate results. Our rounding calculator follows these established mathematical principles:
Standard Rounding Rules
- Identify which place value you want to round to (ones, tenths, hundredths, etc.)
- Look at the digit immediately to the right of this place value
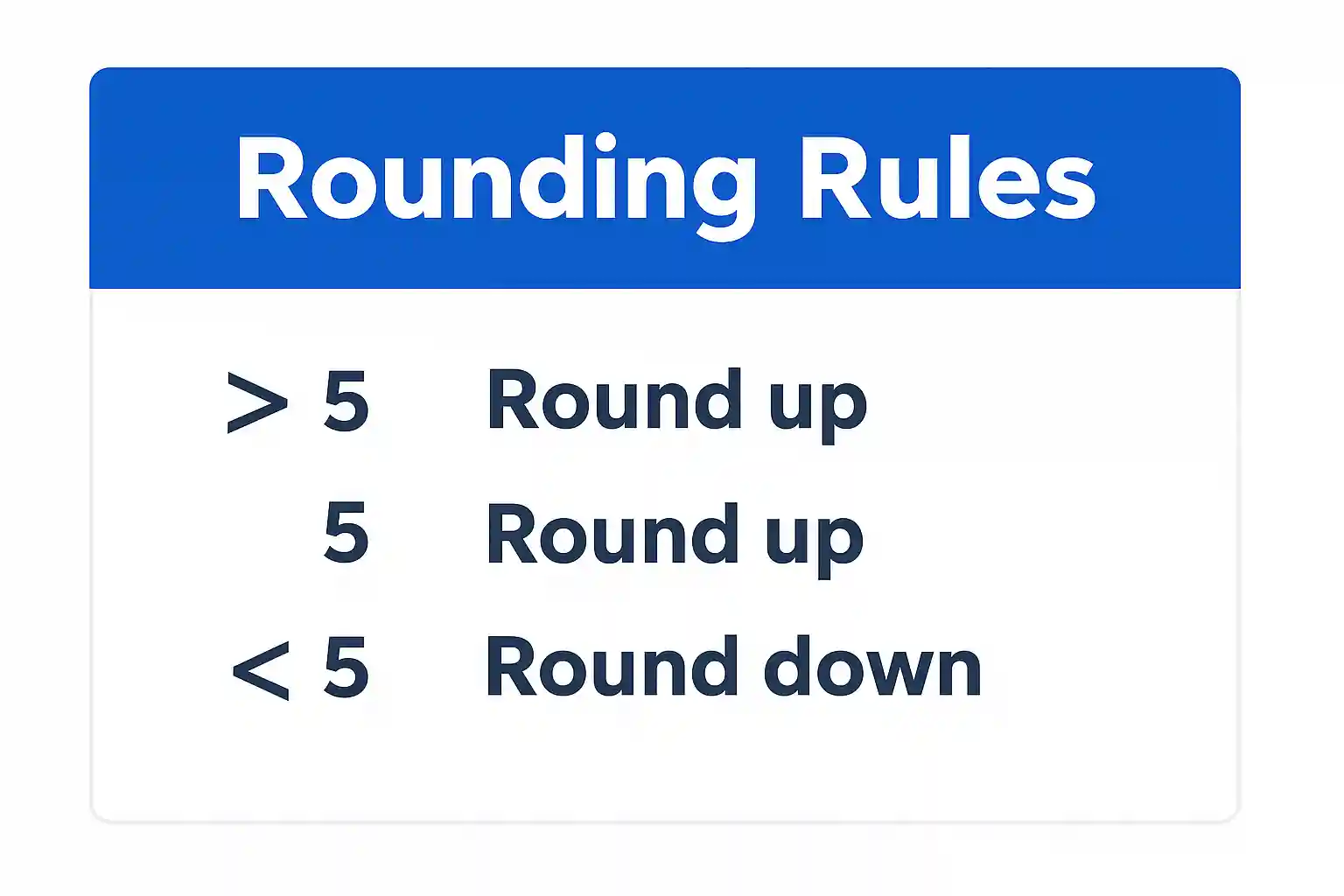
- If that digit is less than 5 (0, 1, 2, 3, or 4), round down by leaving the target digit unchanged
- If that digit is 5 or greater (5, 6, 7, 8, or 9), round up by increasing the target digit by 1
- Replace all digits to the right of the rounding position with zeros (or drop them if they’re after the decimal point)
Remember: The digit to the right of your target position is the only one that matters when determining whether to round up or down.
Examples of Rounding to Different Decimal Places
Let’s explore some practical examples of rounding numbers to different decimal places. Our rounding calculator can handle all these scenarios instantly, but understanding the process helps build your mathematical intuition.
| Original Number | Rounding To | Result | Explanation |
| 3.14159 | Nearest whole number | 3 | Since 0.14159 |
| 7.85 | Nearest whole number | 8 | Since 0.85 > 0.5, round up |
| 42.352 | Nearest tenth | 42.4 | Since 5 ≥ 5, round up |
| 0.6749 | Nearest hundredth | 0.67 | Since 4 |
| 1234.5678 | Nearest thousand | 1000 | Since 234.5678 |
Rounding to Significant Figures
Rounding to significant figures differs from rounding to decimal places. Significant figures (or significant digits) are the digits in a number that carry meaningful value contributing to its precision. Our rounding calculator can handle both decimal place rounding and significant figure rounding.

How to Identify Significant Figures
- All non-zero digits are significant (1, 2, 3, etc.)
- Zeros between non-zero digits are significant (e.g., in 1.05, the 0 is significant)
- Leading zeros (zeros before the first non-zero digit) are never significant
- Trailing zeros in a number with a decimal point are significant
- Trailing zeros in a whole number may or may not be significant depending on context
Examples of Rounding to Significant Figures
| Original Number | Significant Figures | Result | Explanation |
| 3.14159 | 3 | 3.14 | Keep only the first 3 significant digits |
| 0.00456 | 2 | 0.0046 | Leading zeros are not significant |
| 5280 | 2 | 5300 | Round to 2 significant figures |
Different Rounding Methods
While standard rounding is the most common approach, several other rounding methods exist for specific applications. Our rounding calculator supports multiple rounding methods to suit your needs.
Rounding Up (Ceiling)
Always rounds a number up to the next specified place value, regardless of the digits that follow. This method is useful when you need to ensure you have enough resources.
Example: 3.14 rounded up to the nearest whole number is 4.
Rounding Down (Floor)
Always rounds a number down to the previous specified place value, regardless of the digits that follow. This is useful when you need to stay within a certain limit.
Example: 3.94 rounded down to the nearest whole number is 3.
Banker’s Rounding
Also known as unbiased rounding, this method rounds to the nearest even number when the digit is exactly 5. This reduces bias in statistical sampling.
Example: 2.5 rounds to 2, while 3.5 rounds to 4.
Real-World Applications of Rounding
Rounding numbers is essential in numerous fields and everyday situations. Understanding when and how to round appropriately can significantly impact decision-making and communication.
Finance and Accounting
- Rounding monetary values to the nearest cent
- Financial reporting and budget estimations
- Tax calculations and interest rates
Science and Engineering
- Reporting measurements with appropriate precision
- Significant figures in scientific calculations
- Engineering tolerances and specifications
Everyday Applications
- Estimating costs when shopping
- Measuring ingredients in cooking
- Time management and scheduling
The appropriate rounding method and precision depend on the specific application. In some cases, rounding too much can lead to significant errors, while in others, excessive precision is unnecessary.
Tips and Best Practices for Accurate Rounding
To ensure your rounded numbers are both accurate and appropriate for your specific needs, follow these best practices:
Maintain Consistency
Use the same rounding method and precision throughout a single analysis or document to ensure consistency in your results.
Choose Appropriate Precision
Consider the context and purpose of your calculation. Financial calculations might require rounding to the nearest cent, while rough estimates might only need the nearest whole number.
Document Your Rounding Method
When presenting rounded numbers in professional or academic contexts, clearly state which rounding method and precision you used.
Avoid Multiple Roundings
Perform all necessary calculations with full precision first, then round the final result. Rounding intermediate values can compound errors.
Consider Cumulative Effects
Be aware that rounding can introduce bias when working with large datasets. Methods like banker’s rounding can help mitigate this.
Use a Reliable Tool
A dedicated rounding calculator ensures consistent application of rounding rules and eliminates human error in the process.
Frequently Asked Questions About Rounding
What is the difference between rounding and truncating?
Rounding follows specific rules to approximate a number to a certain precision, considering the value of the digit to the right of the rounding position. Truncating simply removes all digits beyond a certain point without any adjustments, essentially always rounding down.
How do I round to the nearest whole number?
To round to the nearest whole number, look at the first digit after the decimal point. If it’s less than 5, round down by keeping the whole number as is. If it’s 5 or greater, round up by adding 1 to the whole number. For example, 3.4 rounds to 3, while 3.5 rounds to 4.
What is banker’s rounding and when should I use it?
Banker’s rounding (also called rounding to even) rounds numbers that end in 5 to the nearest even number. For example, 2.5 rounds to 2, while 3.5 rounds to 4. This method is used in financial and statistical applications to reduce bias that can accumulate when rounding many numbers in the same direction.
How does rounding affect accuracy in calculations?
Rounding introduces a small amount of error into calculations. When working with many rounded numbers or performing multiple calculations with rounded values, these errors can compound. For maximum accuracy, perform all calculations with full precision first, then round only the final result.
How do I round negative numbers?
Negative numbers follow the same rounding rules as positive numbers. Look at the absolute value, apply the rounding rules, then reapply the negative sign. For example, -3.7 rounds to -4 (away from zero), while -3.2 rounds to -3 (toward zero).
Master Rounding with Our Free Calculator
Whether you’re a student, professional, or just need to round numbers accurately, our rounding calculator makes the process simple and error-free.
Conclusion
Rounding numbers is a fundamental mathematical skill with applications across numerous fields and everyday situations. By understanding the basic rules of rounding, different rounding methods, and when to apply them, you can ensure your calculations are both accurate and appropriate for your specific needs.
Our rounding calculator simplifies this process by automatically applying the correct rounding rules to any number, saving you time and eliminating the potential for human error. Whether you’re rounding to the nearest whole number, decimal place, or significant figure, our calculator provides instant, accurate results.
Remember that the appropriate level of precision depends on your specific application. In some contexts, excessive precision can be misleading, while in others, rounding too much can lead to significant errors. Always consider the purpose of your calculation when deciding how to round your numbers.