Permutation and Combination Calculator helps you find arrangements and selections quickly. Fast, accurate tool for math, probability, and combinatorics problems.
Permutation and Combination Calculator
When faced with counting possibilities in complex scenarios, understanding permutations and combinations becomes essential. Whether you’re calculating lottery odds, analyzing password security, or determining team selection possibilities, these mathematical concepts provide powerful tools for solving counting problems. Our Permutation and Combination Calculator simplifies these calculations, helping you navigate the intricate world of combinatorial mathematics with ease and precision.
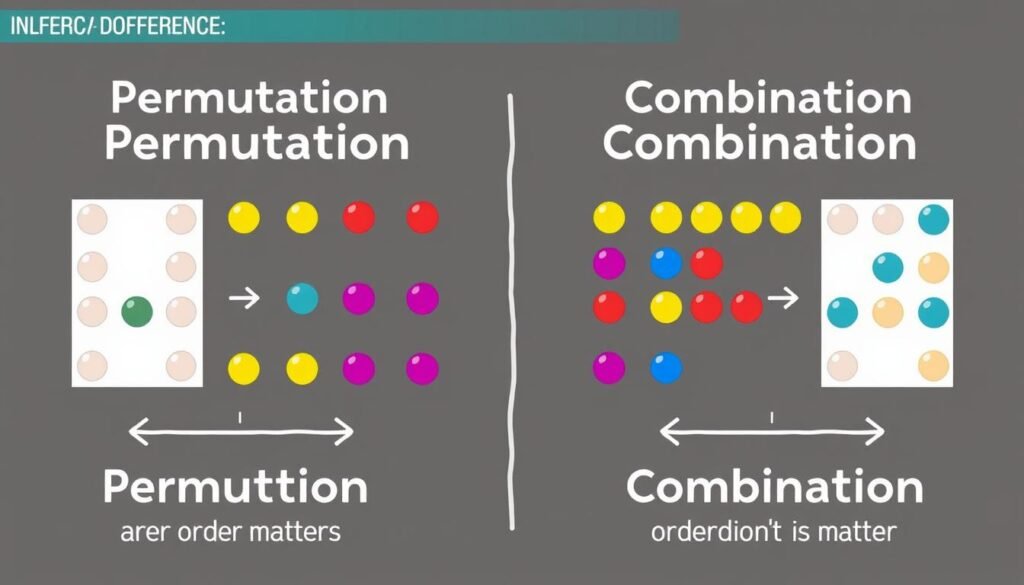
Permutations consider the order of elements, while combinations focus only on which elements are selected
Understanding Permutations and Combinations
Permutations and combinations form the foundation of combinatorics, a branch of mathematics focused on counting, arrangement, and combination of objects within a set. While both concepts involve selecting elements from a larger set, they differ in one crucial aspect: order.
What is a Permutation?
A permutation is an arrangement of objects where order matters. When calculating permutations, we’re counting the number of ways to arrange a selection of elements in a specific sequence.
For example, the lock combination “1-2-3” is different from “3-2-1” because the order of digits matters. Each different arrangement represents a distinct permutation.
What is a Combination?
A combination is a selection of objects where order doesn’t matter. When calculating combinations, we’re counting the number of ways to select elements regardless of their arrangement.
For example, when selecting a team of 3 players from a group of 10, it doesn’t matter which player is selected first, second, or third – only which 3 players are on the team.
Essential Formulas for Permutations and Combinations
The fundamental formulas for calculating permutations and combinations
Permutation Formula
The formula for calculating permutations of n distinct objects taken r at a time is:
P(n,r) = n! / (n – r)!
Where n! (n factorial) represents the product of all positive integers less than or equal to n.
Example: How many different 3-digit numbers can be formed using the digits 1, 2, 3, 4, and 5 without repetition?
Here, n = 5 (total digits available) and r = 3 (digits needed)
P(5,3) = 5! / (5 – 3)! = 5! / 2! = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 120 / 2 = 60
Therefore, 60 different 3-digit numbers can be formed.
Combination Formula
The formula for calculating combinations of n distinct objects taken r at a time is:
C(n,r) = n! / [r! × (n – r)!]
This is also known as the binomial coefficient and is sometimes written as nCr or (n choose r).
Example: In how many ways can a committee of 3 people be formed from a group of 8 people?
Here, n = 8 (total people available) and r = 3 (committee size)
C(8,3) = 8! / [3! × (8 – 3)!] = 8! / [3! × 5!] = (8 × 7 × 6 × 5!) / [3 × 2 × 1 × 5!] = 336 / 6 = 56
Therefore, 56 different committees can be formed.
Step-by-Step Calculation Guide
Breaking down the calculation process into manageable steps
Calculating Permutations Manually
- Identify the total number of objects (n) and how many you’re selecting (r)
- Calculate n! (multiply all integers from n down to 1)
- Calculate (n-r)! (multiply all integers from (n-r) down to 1)
- Divide n! by (n-r)! to get your answer
When calculating factorials for large numbers, you can simplify by canceling out common factors. For example, when finding P(8,3), instead of calculating 8!/5! completely, you can simplify to 8 × 7 × 6, since the 5! terms cancel out.
Calculating Combinations Manually
- Identify the total number of objects (n) and how many you’re selecting (r)
- Calculate n! (multiply all integers from n down to 1)
- Calculate r! (multiply all integers from r down to 1)
- Calculate (n-r)! (multiply all integers from (n-r) down to 1)
- Divide n! by the product of r! and (n-r)! to get your answer
For large calculations, you can use the formula C(n,r) = C(n,n-r) to potentially simplify your work. For example, C(50,48) is the same as C(50,2), which is much easier to calculate.
Real-World Applications of Permutations and Combinations
Permutations and combinations have numerous practical applications across different fields
Probability and Statistics
Permutations and combinations form the foundation of probability theory. When calculating the probability of specific outcomes in events like card draws, dice rolls, or lottery selections, these concepts help determine the total number of possible outcomes and favorable outcomes.
Probability calculations often rely on permutation and combination principles
Cryptography and Security
Password security, encryption algorithms, and cryptographic systems all rely on combinatorial mathematics. The strength of a password or encryption key is often measured by the number of possible combinations, making permutation and combination calculations essential for cybersecurity.
Genetics and Biology
In genetics, combinations help calculate the possible genetic outcomes from parental genes. Scientists use combinatorial mathematics to analyze DNA sequences, protein structures, and genetic variations across populations.
Genetic research relies heavily on combinatorial mathematics
Business and Operations Research
Businesses use combinations and permutations for inventory management, scheduling, logistics optimization, and market research. These concepts help analyze possible product configurations, service offerings, and resource allocations.
Common Permutation and Combination Problems
Understanding problem types helps identify the correct calculation approach
The Handshake Problem
In a group of n people, if each person shakes hands with everyone else exactly once, how many handshakes occur in total?
This is a classic combination problem, as the order of who shakes whose hand doesn’t matter. The formula is C(n,2) = n(n-1)/2.
For example, in a group of 10 people, there would be C(10,2) = 10 × 9 / 2 = 45 handshakes.
The Committee Selection Problem
From a group of n people, how many different committees of r people can be formed?
Since the order of selection doesn’t matter, this is a combination problem with the formula C(n,r).
For example, selecting a committee of 4 from 12 people gives C(12,4) = 12! / [4! × 8!] = 495 possible committees.
The Arrangement Problem
In how many ways can n different objects be arranged in a row?
This is a permutation problem where we’re selecting all n objects, so the formula is P(n,n) = n!.
For example, arranging 5 different books on a shelf gives P(5,5) = 5! = 120 possible arrangements.
The Word Formation Problem
How many different words (meaningful or not) can be formed using all the letters of a given word?
If all letters are different, this is P(n,n) = n!. If some letters repeat, divide by the factorial of each letter’s frequency.
For example, “MATH” has 4 different letters, so there are 4! = 24 possible arrangements.
A dedicated calculator saves time and ensures accuracy for complex calculations
Why Use a Permutation and Combination Calculator?
Time Efficiency
Manual calculations of permutations and combinations can be time-consuming, especially with large numbers. A specialized calculator performs these calculations instantly, saving valuable time for students, researchers, and professionals.
Accuracy Guarantee
Factorial calculations can quickly become complex, increasing the risk of computational errors. A dedicated calculator eliminates these risks, providing precise results every time, even for problems involving large numbers.
Educational Value
Beyond providing answers, a good permutation and combination calculator helps users understand the underlying concepts by showing step-by-step solutions and formula applications, enhancing the learning experience.
Explore Our Other Mathematical Tools
Enhance your mathematical problem-solving capabilities with our comprehensive suite of calculators designed for students, educators, and professionals.
Practical Examples and Solutions
Working through examples helps solidify understanding of these concepts
Lottery Problem
Question: In a lottery where you select 6 numbers from 49, how many different combinations are possible?
Solution: Since the order of the numbers doesn’t matter, this is a combination problem.
C(49,6) = 49! / [6! × (49-6)!] = 49! / [6! × 43!]
= (49 × 48 × 47 × 46 × 45 × 44 × 43!) / [6 × 5 × 4 × 3 × 2 × 1 × 43!]
= 13,983,816
This explains why winning the lottery is so difficult – you have a 1 in nearly 14 million chance!
Password Security Problem
Question: How many possible 8-character passwords can be created using lowercase letters (a-z) and digits (0-9)?
Solution: This is a permutation with repetition allowed. We have 26 letters and 10 digits, so 36 possible characters for each position.
Total possibilities = 368 = 2,821,109,907,456
That’s over 2.8 trillion possible passwords, demonstrating why longer passwords with varied character types are more secure.
Team Selection Problem
Question: A basketball coach needs to select 5 starting players from a team of 12. How many different starting lineups are possible?
Solution: Since the order doesn’t matter (we just need to know which 5 players are starting), this is a combination problem.
C(12,5) = 12! / [5! × (12-5)!] = 12! / [5! × 7!]
= (12 × 11 × 10 × 9 × 8 × 7!) / [5 × 4 × 3 × 2 × 1 × 7!]
= 792
The coach has 792 different possible starting lineups to consider!
Related Mathematical Concepts
Permutations and combinations connect to many other mathematical areas
Factorial Calculations
Factorials (n!) are fundamental to both permutation and combination formulas. Understanding factorial properties and calculations is essential for mastering combinatorial mathematics.
Binomial Theorem
The binomial theorem uses combinations (binomial coefficients) to expand expressions of the form (x + y)n. This connection highlights the importance of combinations in algebra and calculus.
Probability Distributions
Many probability distributions, including the binomial and hypergeometric distributions, are built on combinatorial foundations, using permutations and combinations to calculate probabilities.
Explore Related Calculators
Deepen your understanding of mathematical concepts with our specialized calculators
Mastering Permutations and Combinations
Understanding these concepts opens doors to solving complex counting problems
Permutations and combinations provide powerful tools for solving counting problems across numerous fields. By understanding when order matters (permutations) and when it doesn’t (combinations), you can tackle complex probability questions, analyze possible outcomes, and make informed decisions based on mathematical principles.
Whether you’re a student learning these concepts for the first time, an educator teaching combinatorial mathematics, or a professional applying these principles in your work, mastering permutations and combinations enhances your problem-solving capabilities and mathematical reasoning.
Our Permutation and Combination Calculator simplifies these calculations, allowing you to focus on understanding the concepts and their applications rather than getting lost in complex factorial arithmetic. By leveraging this tool alongside a solid understanding of the underlying principles, you’ll be well-equipped to solve a wide range of counting problems with confidence and precision.
Ready to Solve More Mathematical Problems?
Explore our complete collection of mathematical calculators designed to simplify complex calculations and enhance your problem-solving skills.