Area Calculator helps you quickly find the area of squares, rectangles, circles, and more. Simple, accurate, and perfect for math and geometry tasks.
Area Calculator
Understanding how to calculate area is essential for numerous real-world applications, from determining how much paint you need for a wall to measuring land for construction projects. This comprehensive guide provides all the formulas, step-by-step examples, and practical applications you need to calculate the area of any shape. Whether you're a student, homeowner, or professional, our area calculator guide will help you solve area problems with confidence.
Need to Calculate Area Quickly?
Use our online area calculator for instant, accurate results for any shape.
What is Area? Understanding the Basics
Area is the measure of the space inside a two-dimensional shape. It represents how much surface the shape covers and is measured in square units (square feet, square meters, etc.). Think of area as the amount of paint needed to cover a surface or the size of a piece of land.
Different shapes can have the same area of 12 square units
Unlike perimeter (which measures the distance around a shape), area measures the space contained within the boundaries of a shape. Understanding area is crucial for many practical applications, from construction and interior design to agriculture and land management.
Common Area Measurement Units
Area can be expressed in various units depending on the application and region. Here are the most common area units you'll encounter:
| Unit | Symbol | Equivalent in Square Meters | Common Uses |
| Square Meter | m² | 1 m² | Standard SI unit, building interiors |
| Square Foot | ft² | 0.0929 m² | Real estate, room dimensions (US) |
| Square Yard | yd² | 0.8361 m² | Carpeting, landscaping |
| Acre | ac | 4,046.9 m² | Land measurement, real estate |
| Hectare | ha | 10,000 m² | Agriculture, forestry |
| Square Kilometer | km² | 1,000,000 m² | Geographic regions, countries |
| Square Mile | mi² | 2,589,988 m² | Large land areas, cities |
Converting between area units is essential when working with different measurement systems. For example, to convert square feet to square meters, multiply by 0.0929. To convert acres to square feet, multiply by 43,560.
How to Calculate the Area of a Square
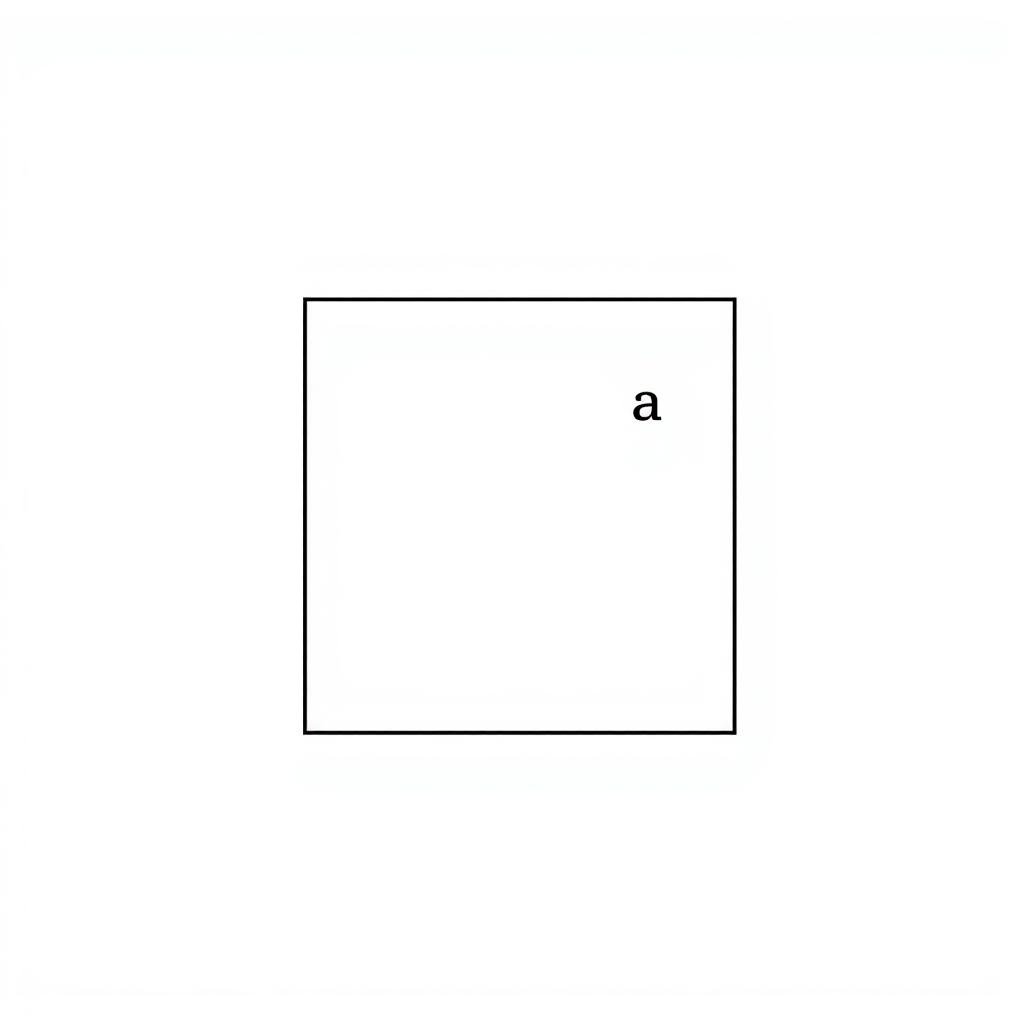
A square has four equal sides and four right angles (90°). Calculating its area is straightforward:
Square Area Formula: A = a²
Where 'a' is the length of one side of the square.
Example Calculation:
If a square has sides of 5 meters, its area would be:
A = 5² = 5 × 5 = 25 square meters (m²)
Real-World Application:
Imagine you need to tile a square bathroom floor that measures 8 feet on each side. To calculate how many square feet of tiles you'll need:
A = 8² = 8 × 8 = 64 square feet (ft²)
How to Calculate the Area of a Rectangle

A rectangle has four sides with opposite sides being equal in length, and four right angles. The formula for calculating the area of a rectangle is:
Rectangle Area Formula: A = l × w
Where 'l' is the length and 'w' is the width of the rectangle.
Example Calculation:
If a rectangle has a length of 10 meters and a width of 6 meters, its area would be:
A = 10 × 6 = 60 square meters (m²)
Real-World Application:
When calculating how much carpet you need for a living room that measures 15 feet long by 12 feet wide:
A = 15 × 12 = 180 square feet (ft²)
Save Time on Complex Calculations
Our area calculator handles all formulas automatically - just enter your measurements.
How to Calculate the Area of a Triangle
Triangles are three-sided polygons, and there are several ways to calculate their area depending on what information you have available.
Triangle Area Formula (Base and Height): A = (b × h) ÷ 2
Where 'b' is the base length and 'h' is the height (perpendicular distance from the base to the opposite vertex).
Example Calculation:
If a triangle has a base of 8 meters and a height of 6 meters, its area would be:
A = (8 × 6) ÷ 2 = 48 ÷ 2 = 24 square meters (m²)
Alternative Triangle Area Formulas:
Heron's Formula (Three Sides Known):
A = √(s(s-a)(s-b)(s-c))
Where s = (a+b+c)/2 (half the perimeter)
This is useful when you know all three sides but not the height.
SAS Formula (Two Sides and Included Angle):
A = (1/2) × a × b × sin(C)
Where 'a' and 'b' are two sides and 'C' is the angle between them.
Real-World Application:
When calculating the area of a triangular garden plot with a base of 12 feet and a height of 8 feet:
A = (12 × 8) ÷ 2 = 96 ÷ 2 = 48 square feet (ft²)
How to Calculate the Area of a Circle
A circle is a perfectly round shape where all points on the edge are the same distance (radius) from the center point.
Circle Area Formula: A = πr²
Where 'r' is the radius of the circle and π (pi) is approximately 3.14159.
Example Calculation:
If a circle has a radius of 5 meters, its area would be:
A = π × 5² = 3.14159 × 25 ≈ 78.54 square meters (m²)
If you know the diameter (d) instead of the radius, remember that radius = diameter ÷ 2, so the formula becomes:
A = π × (d/2)²
Real-World Application:
When determining how much fertilizer is needed for a circular garden with a radius of 3 feet:
A = π × 3² = 3.14159 × 9 ≈ 28.27 square feet (ft²)
How to Calculate the Area of a Trapezoid
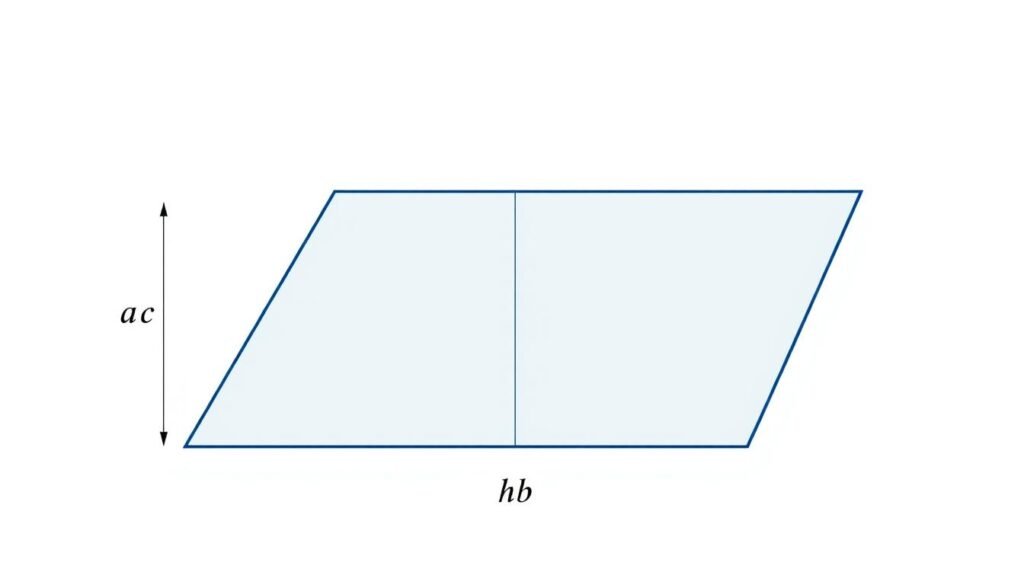
A trapezoid (also called a trapezium in some countries) is a quadrilateral with exactly one pair of parallel sides.
Trapezoid Area Formula: A = ((a + b) × h) ÷ 2
Where 'a' and 'b' are the lengths of the parallel sides and 'h' is the height (perpendicular distance between the parallel sides).
Example Calculation:
If a trapezoid has parallel sides of 10 meters and 6 meters, with a height of 4 meters, its area would be:
A = ((10 + 6) × 4) ÷ 2 = (16 × 4) ÷ 2 = 64 ÷ 2 = 32 square meters (m²)
Real-World Application:
When calculating the area of a trapezoidal garden bed with parallel sides of 8 feet and 12 feet, and a height of 5 feet:
A = ((8 + 12) × 5) ÷ 2 = (20 × 5) ÷ 2 = 100 ÷ 2 = 50 square feet (ft²)
How to Calculate the Area of a Parallelogram
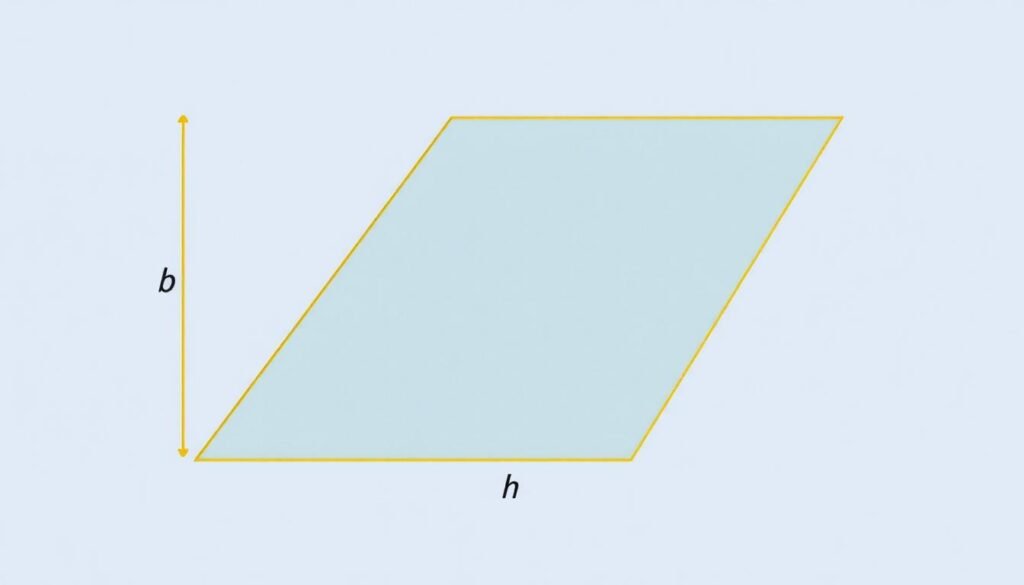
A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
Parallelogram Area Formula: A = b × h
Where 'b' is the base length and 'h' is the height (perpendicular distance from the base to the opposite side).
Example Calculation:
If a parallelogram has a base of 8 meters and a height of 5 meters, its area would be:
A = 8 × 5 = 40 square meters (m²)
Real-World Application:
When designing a parallelogram-shaped garden with a base of 15 feet and a height of 10 feet:
A = 15 × 10 = 150 square feet (ft²)
Calculate Complex Shapes Easily
From circles to polygons, our area calculator handles all shapes with precision.
How to Calculate the Area of an Ellipse
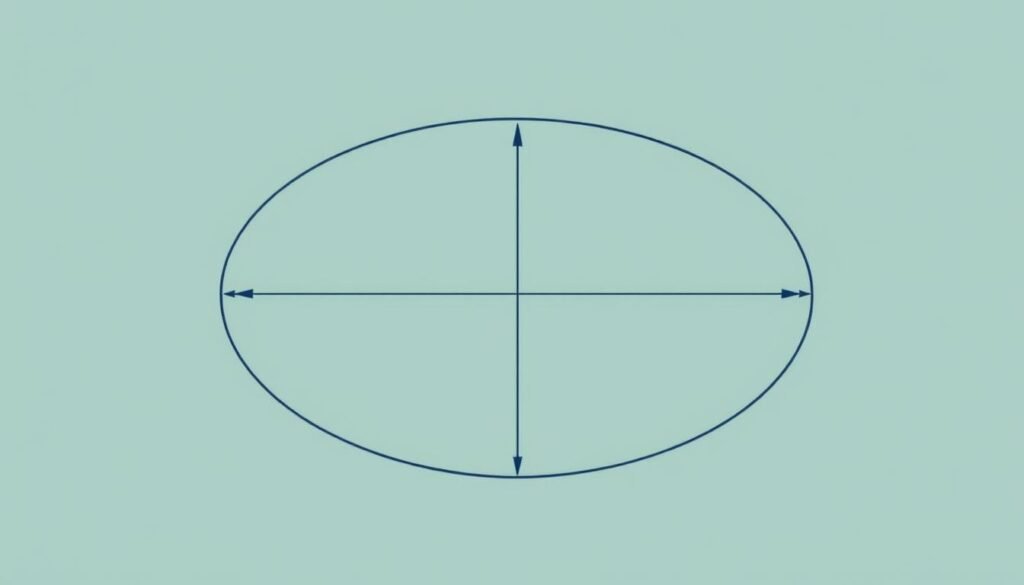
An ellipse is a curved shape where the sum of distances from any point on the curve to two fixed points (foci) is constant.
Ellipse Area Formula: A = π × a × b
Where 'a' is the semi-major axis (half the longest diameter) and 'b' is the semi-minor axis (half the shortest diameter).
Example Calculation:
If an ellipse has a semi-major axis of 6 meters and a semi-minor axis of 4 meters, its area would be:
A = π × 6 × 4 = 3.14159 × 24 ≈ 75.4 square meters (m²)
Real-World Application:
When calculating the area of an elliptical garden with a longest diameter of 14 feet and a shortest diameter of 10 feet:
Semi-major axis = 14 ÷ 2 = 7 feet
Semi-minor axis = 10 ÷ 2 = 5 feet
A = π × 7 × 5 = 3.14159 × 35 ≈ 110 square feet (ft²)
How to Calculate the Area of a Sector
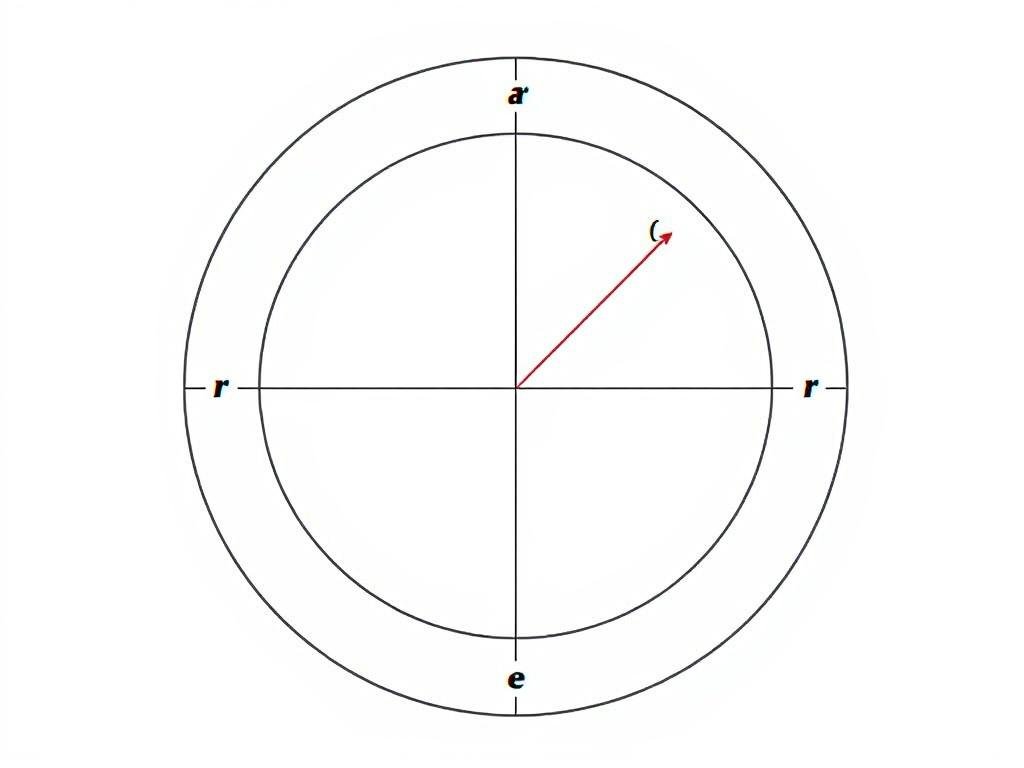
A sector is a portion of a circle enclosed by two radii and an arc. Think of it as a "pizza slice" shape.
Sector Area Formula: A = (θ ÷ 360°) × πr²
Where 'r' is the radius of the circle and 'θ' is the central angle in degrees.
Example Calculation:
If a sector has a radius of 6 meters and a central angle of 45 degrees, its area would be:
A = (45 ÷ 360) × π × 6² = 0.125 × 3.14159 × 36 ≈ 14.14 square meters (m²)
Real-World Application:
When calculating the area of a sector-shaped garden bed with a radius of 8 feet and a central angle of 60 degrees:
A = (60 ÷ 360) × π × 8² = (1/6) × 3.14159 × 64 ≈ 33.51 square feet (ft²)
How to Calculate the Area of Regular Polygons
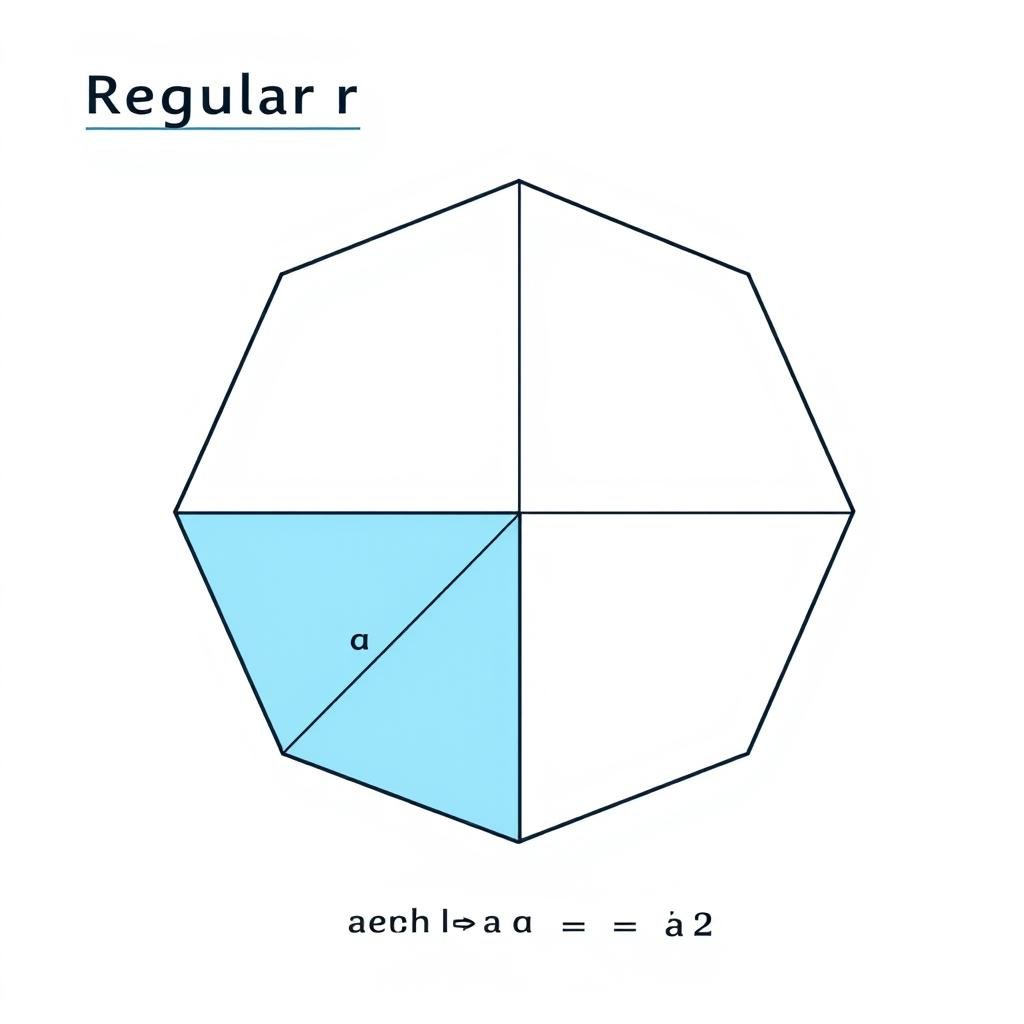
Pentagon (5 sides)
A = (5 × a²) ÷ (4 × tan(π/5))
Where 'a' is the side length

Hexagon (6 sides)
A = (6 × a²) ÷ (4 × tan(π/6))
Where 'a' is the side length

Octagon (8 sides)
A = (8 × a²) ÷ (4 × tan(π/8))
Where 'a' is the side length
For any regular polygon with 'n' sides, the general formula is:
Regular Polygon Area Formula: A = (n × a²) ÷ (4 × tan(π/n))
Where 'n' is the number of sides and 'a' is the side length.
Example Calculation:
If a regular hexagon has sides of 5 meters, its area would be:
A = (6 × 5²) ÷ (4 × tan(π/6)) = (6 × 25) ÷ (4 × 0.5774) ≈ 150 ÷ 2.3096 ≈ 64.95 square meters (m²)
How to Calculate the Area of Irregular Shapes
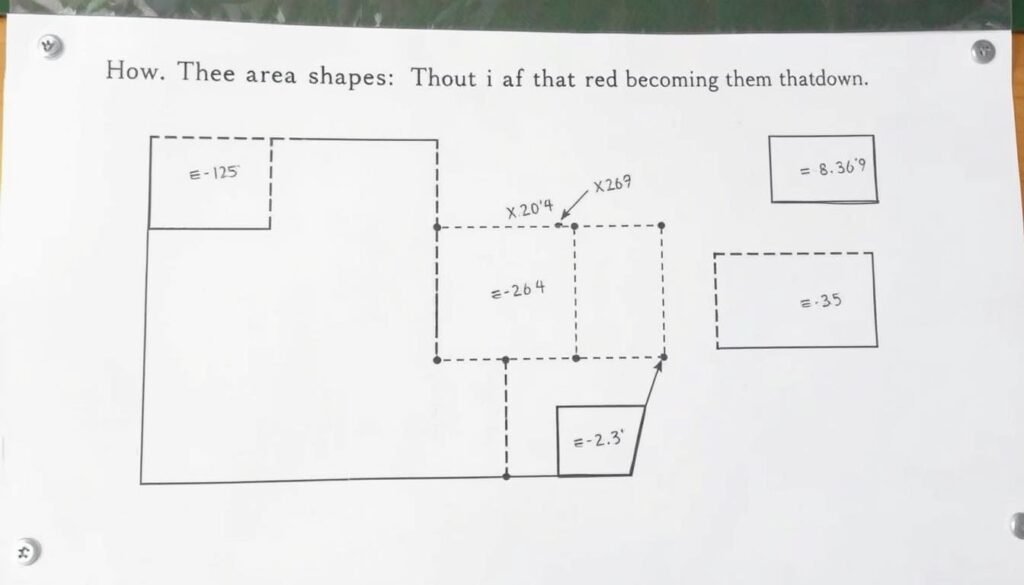
For irregular shapes, the best approach is to divide the shape into simpler shapes (triangles, rectangles, etc.), calculate the area of each, and then add them together.
Step-by-Step Process:
- Divide the irregular shape into simple shapes like triangles, rectangles, and circles.
- Calculate the area of each simple shape using the appropriate formula.
- Add all the individual areas together to find the total area.
- If there are parts that overlap or need to be subtracted, subtract those areas.
Example Calculation:
Imagine an L-shaped room that can be divided into two rectangles:
- Rectangle 1: 10 feet × 8 feet = 80 square feet
- Rectangle 2: 6 feet × 5 feet = 30 square feet
- Total area = 80 + 30 = 110 square feet
Real-World Application:
When calculating the area of an irregularly shaped garden or property, surveyors often divide it into triangles and other simple shapes, then add the areas together for an accurate measurement.
Measure Any Shape with Precision
Our area calculator handles even the most complex shapes with ease.
Practical Applications of Area Calculations

Home Improvement
- Calculating flooring materials (tile, carpet, hardwood)
- Determining paint needed for walls and ceilings
- Measuring for wallpaper and other wall coverings
- Sizing windows, doors, and other fixtures

Landscaping & Gardening
- Determining mulch, soil, or sod requirements
- Planning garden beds and lawn areas
- Calculating irrigation coverage
- Measuring for fencing and borders

Construction & Real Estate
- Measuring property and land areas
- Calculating concrete needed for foundations
- Determining roof materials
- Assessing living space in homes
Area calculations are also essential in many other fields, including agriculture (crop planning), manufacturing (material requirements), education (teaching geometry), and science (experimental design).
Common Mistakes in Area Calculations
Best Practices
- Double-check all measurements before calculating
- Use consistent units throughout your calculations
- Break complex shapes into simpler components
- Use the correct formula for each shape
- Add a small percentage (5-10%) for waste in practical applications
Common Errors
- Confusing area with perimeter
- Using incorrect formulas for specific shapes
- Mixing different measurement units
- Forgetting to square the radius when calculating circle area
- Not accounting for openings (doors, windows) in practical applications
Remember that area is always expressed in square units (ft², m², etc.). If your answer doesn't have square units, you've likely made a calculation error.
Frequently Asked Questions About Area Calculations
What's the difference between area and perimeter?
Area measures the space inside a shape (in square units), while perimeter measures the distance around the outside of a shape (in linear units). For example, a square with 5-foot sides has an area of 25 square feet and a perimeter of 20 feet.
How do I calculate the area of an irregular shape?
Break the irregular shape into simpler shapes like triangles, rectangles, and circles. Calculate the area of each simple shape, then add them together. For very complex shapes, you might need to use more advanced methods like the trapezoidal rule or Simpson's rule.
What is the formula for calculating the area of a circle?
The formula for calculating the area of a circle is A = πr², where r is the radius of the circle and π (pi) is approximately 3.14159. If you know the diameter (d) instead, the formula becomes A = π(d/2)².
How do I convert between different area units?
To convert between area units, multiply by the appropriate conversion factor. For example, to convert from square feet to square meters, multiply by 0.0929. To convert from acres to square feet, multiply by 43,560.
What's the difference between area and surface area?
Area refers to the space covered by a two-dimensional shape, while surface area refers to the total area of all surfaces of a three-dimensional object. For example, a cube has six square faces, so its surface area is the sum of the areas of all six faces.
Ready to Calculate Area?
Our online area calculator makes it easy to find the area of any shape with precision and speed.
Conclusion: Mastering Area Calculations
Understanding how to calculate area is a valuable skill with countless practical applications. Whether you're a student learning geometry, a homeowner planning renovations, or a professional in construction or landscaping, knowing the right formulas and techniques for area calculation will help you complete your projects accurately and efficiently.
Remember that different shapes require different formulas, and complex shapes can be broken down into simpler components. Always double-check your measurements and calculations, and be consistent with your units.
For quick and accurate results, our area calculator is the perfect tool to handle all your area calculation needs. Simply input your measurements, and get precise results instantly for any shape.