Circle Calculator

Our Circle Calculator provides instant calculations for any circle's area, circumference, radius, and diameter. Whether you're a student working on geometry homework, an engineer designing circular components, or a DIY enthusiast planning a project, this tool eliminates the need for manual calculations and potential errors. Simply input one known value, and our calculator will determine all other measurements automatically.

In this guide, we'll explain all circle properties, provide the essential formulas, and show you how to calculate these values manually. You'll also discover practical applications for circle calculations in everyday life and professional settings.

Understanding Circle Basics

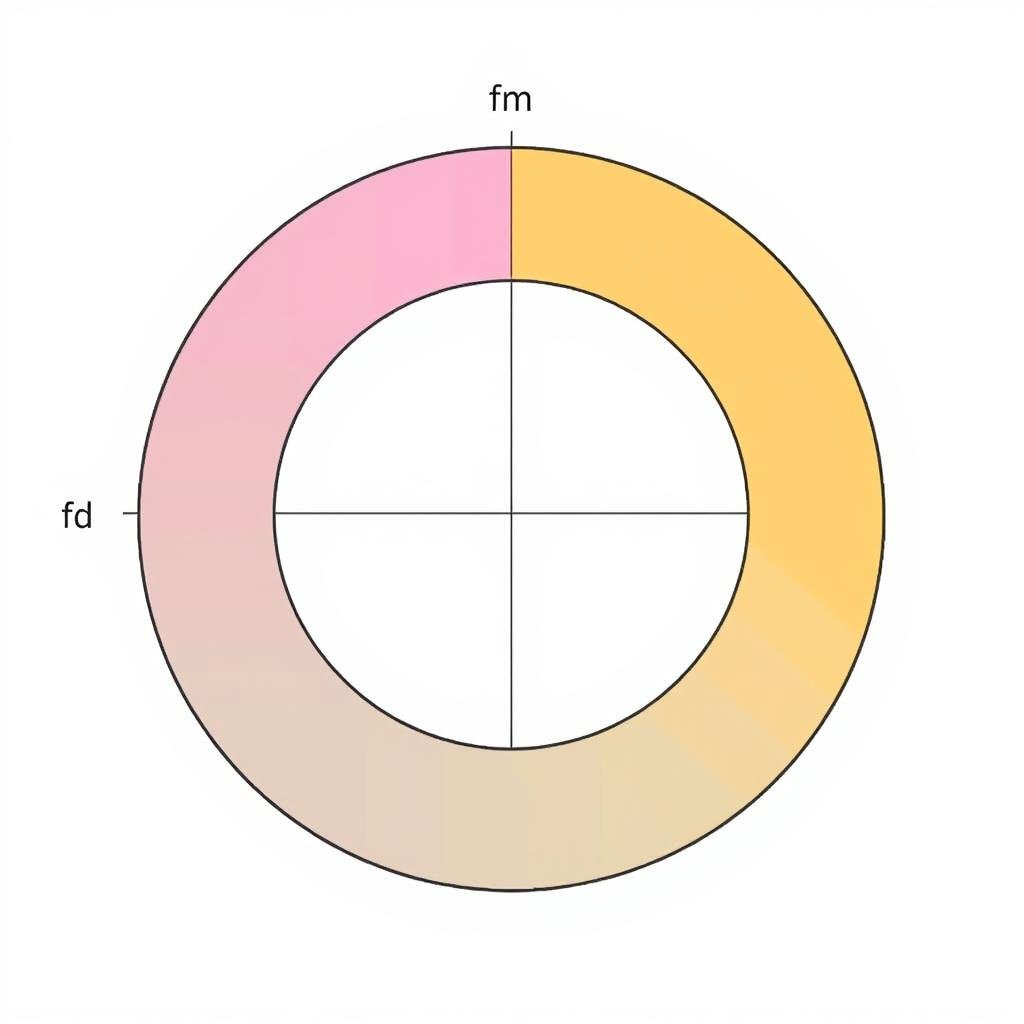
Basic elements of a circle: radius, diameter, circumference, and area

A circle is a perfectly round shape where every point on its edge is the same distance from the center point. This constant distance is called the radius. Understanding the relationship between a circle's radius, diameter, circumference, and area is essential for performing accurate calculations.

Essential Circle Formulas

These fundamental formulas allow you to calculate any circle measurement when you know at least one value. Our Circle Calculator uses these same formulas to provide instant results.

Area of a Circle Formula

The area of a circle represents the space contained within its boundary. The formula for calculating a circle's area is:

A = πr²

If you know the diameter instead of the radius, you can use:

A = π(d/2)² or A = πd²/4

If you know the circumference, you can calculate the area using:

A = C²/(4π)

Step-by-Step Calculation Examples

Let's walk through some practical examples of how to manually calculate different circle measurements. These examples will help you understand how to apply the formulas correctly.

Example 1: Finding Circumference from Radius

Problem: Calculate the circumference of a circle with a radius of 5 cm.

Step 1: Identify the formula for circumference when radius is known.

C = 2πr

Step 2: Substitute the radius value into the formula.

C = 2π × 5 cm

Step 3: Calculate (using π ≈ 3.14).

C = 2 × 3.14 × 5 cm

C = 31.4 cm

Answer: The circumference of the circle is 31.4 cm.

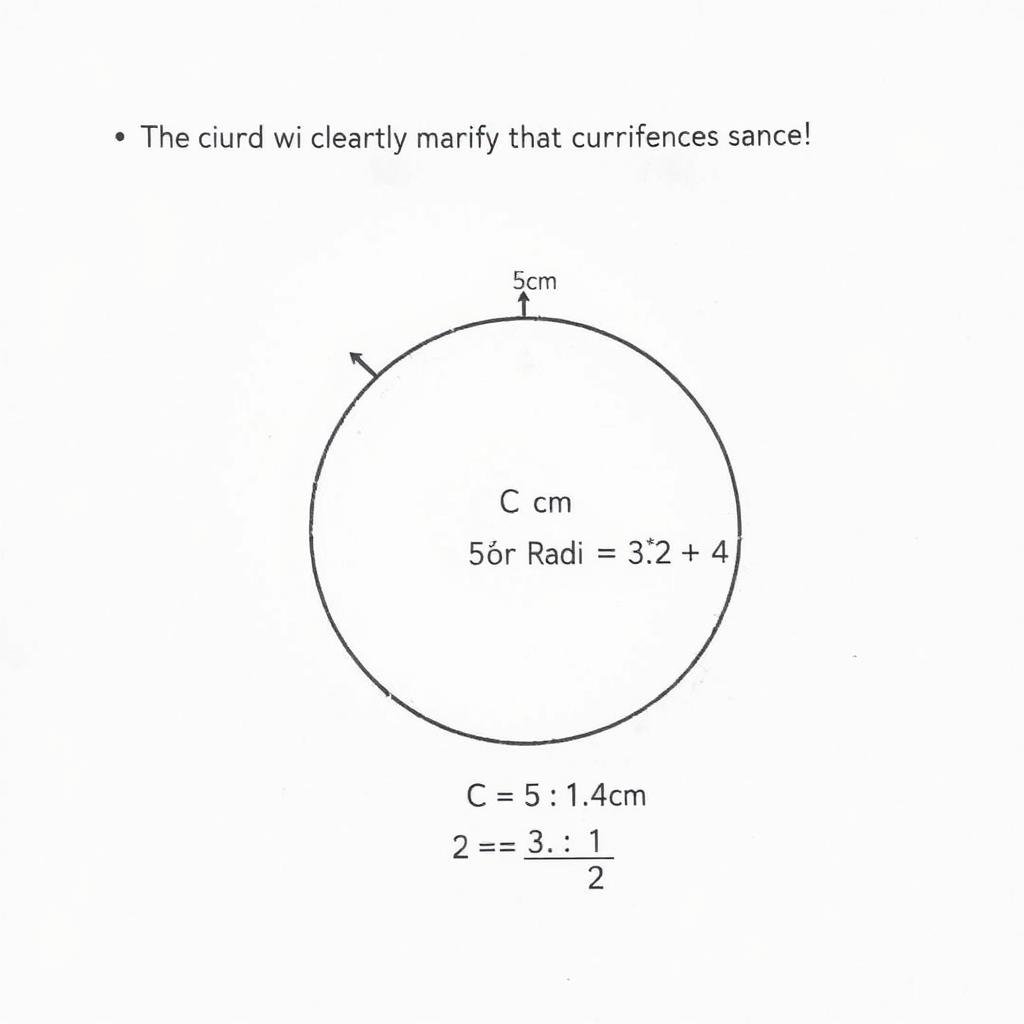
Example 2: Finding Area from Diameter

Problem: Calculate the area of a circle with a diameter of 10 inches.

Step 1: Convert diameter to radius.

r = d/2 = 10/2 = 5 inches

Step 2: Apply the area formula.

A = πr²

A = π × 5² = π × 25

Step 3: Calculate (using π ≈ 3.14).

A = 3.14 × 25 = 78.5 square inches

Answer: The area of the circle is 78.5 square inches.

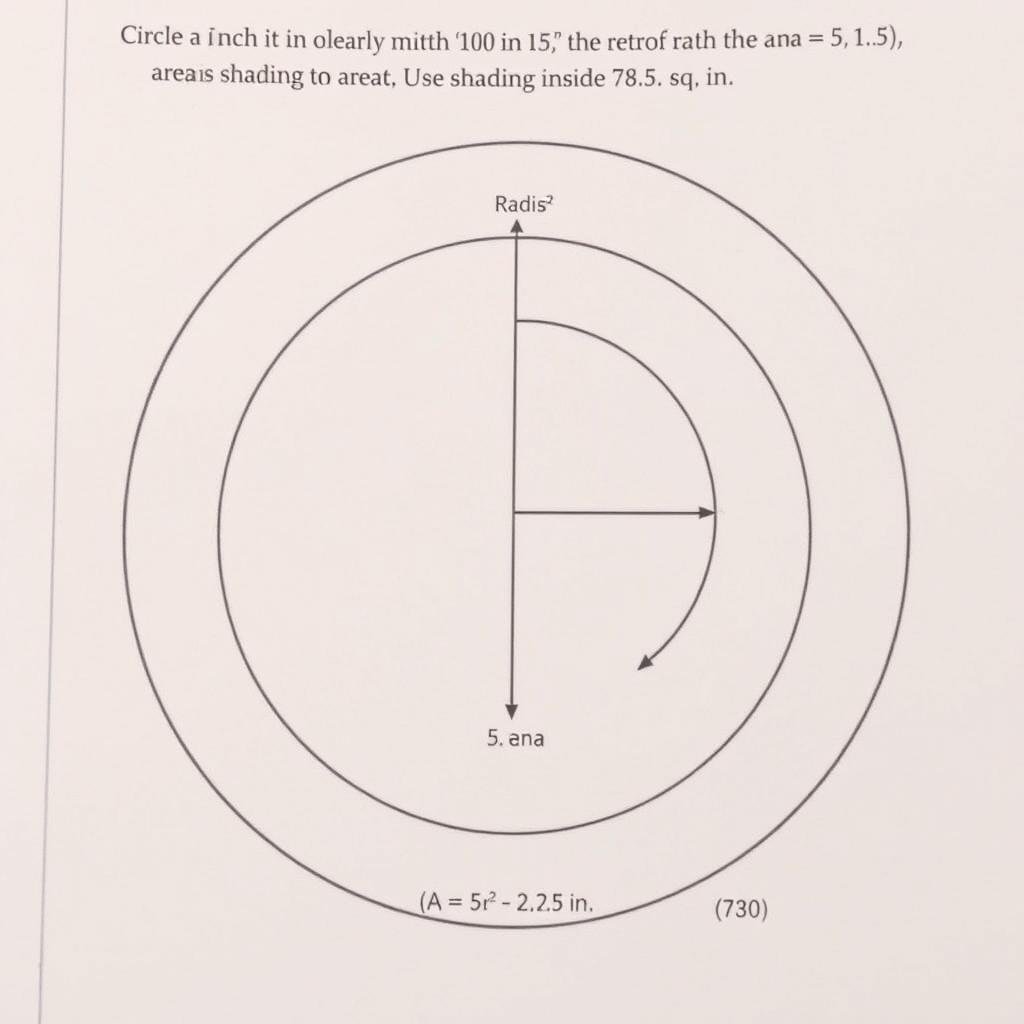
Example 3: Finding Radius from Area

Problem: Find the radius of a circle with an area of 200 square meters.

Step 1: Start with the area formula and solve for radius.

A = πr²

r² = A/π

r = √(A/π)

Step 2: Substitute the area value.

r = √(200/π)

Step 3: Calculate (using π ≈ 3.14).

r = √(200/3.14) = √63.69 = 7.98 meters

Answer: The radius of the circle is approximately 7.98 meters.

Real-World Applications of Circle Calculations

Circle calculations are essential in numerous fields and everyday situations. Here are some common applications where our Circle Calculator can be particularly useful:

Construction & Engineering

• Designing circular foundations, pillars, and structures
• Calculating material requirements for pipes and cylindrical components
• Planning circular rooms, domes, and architectural features
• Determining spacing for circular arrangements (like columns)

Education & Mathematics

• Solving geometry problems and homework assignments
• Teaching fundamental mathematical concepts
• Preparing for math exams and standardized tests
• Demonstrating the practical applications of π (pi)

DIY & Home Projects

• Designing circular garden beds and landscaping features
• Building round tables, fire pits, or decorative elements
• Calculating fabric needed for circular items (tablecloths, rugs)
• Planning space for circular furniture arrangements

Additional Applications

How to Find the Center of a Circle

Finding the center of an existing circle is a common practical problem. Here are two reliable methods you can use:

Method 1: Using Perpendicular Bisectors

1. Draw any two chords (straight lines connecting two points on the circle)
2. Find the midpoint of each chord
3. Draw perpendicular lines through these midpoints
4. The point where these perpendicular lines intersect is the center of the circle

Method 2: Using Right Angles

1. Place a right-angled object (like a carpenter's square) so that it touches the circle at any point
2. Draw two perpendicular lines across the circle from this point
3. Mark where these lines intersect the circle on the opposite sides
4. Connect these points to create a diameter
5. Repeat with another point to create a second diameter
6. The intersection of these diameters is the center of the circle

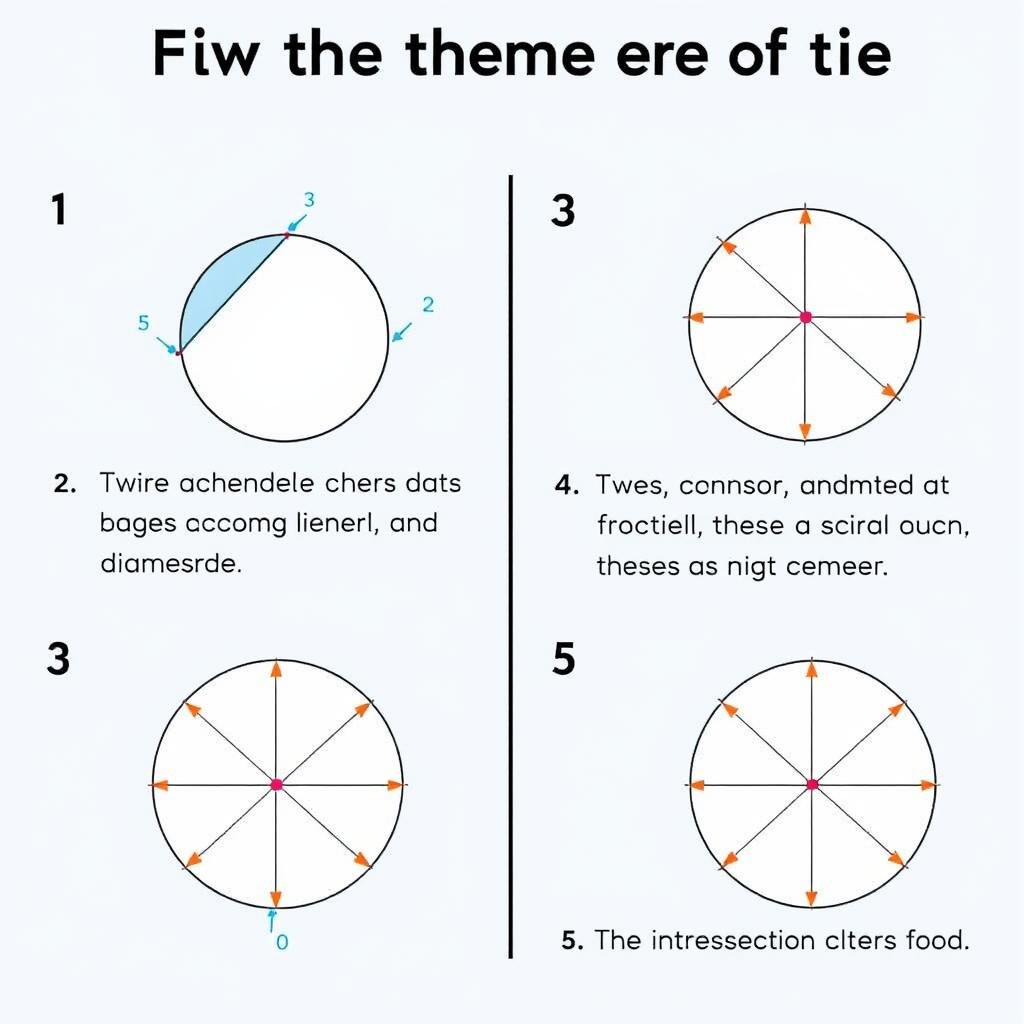
Finding the center of a circle is essential for many practical applications, including construction, design, and crafts. Once you've found the center, you can accurately measure the radius and calculate other circle properties.

Special Types of Circles

Beyond the basic circle, there are several special types and related concepts that are important in mathematics and practical applications:

Unit Circle

A circle with a radius of 1 unit, typically centered at the origin (0,0) on a coordinate plane. The unit circle is fundamental in trigonometry and calculus.

On the unit circle, for any point (x,y):

• x = cos θ
• y = sin θ
• x² + y² = 1

Concentric Circles

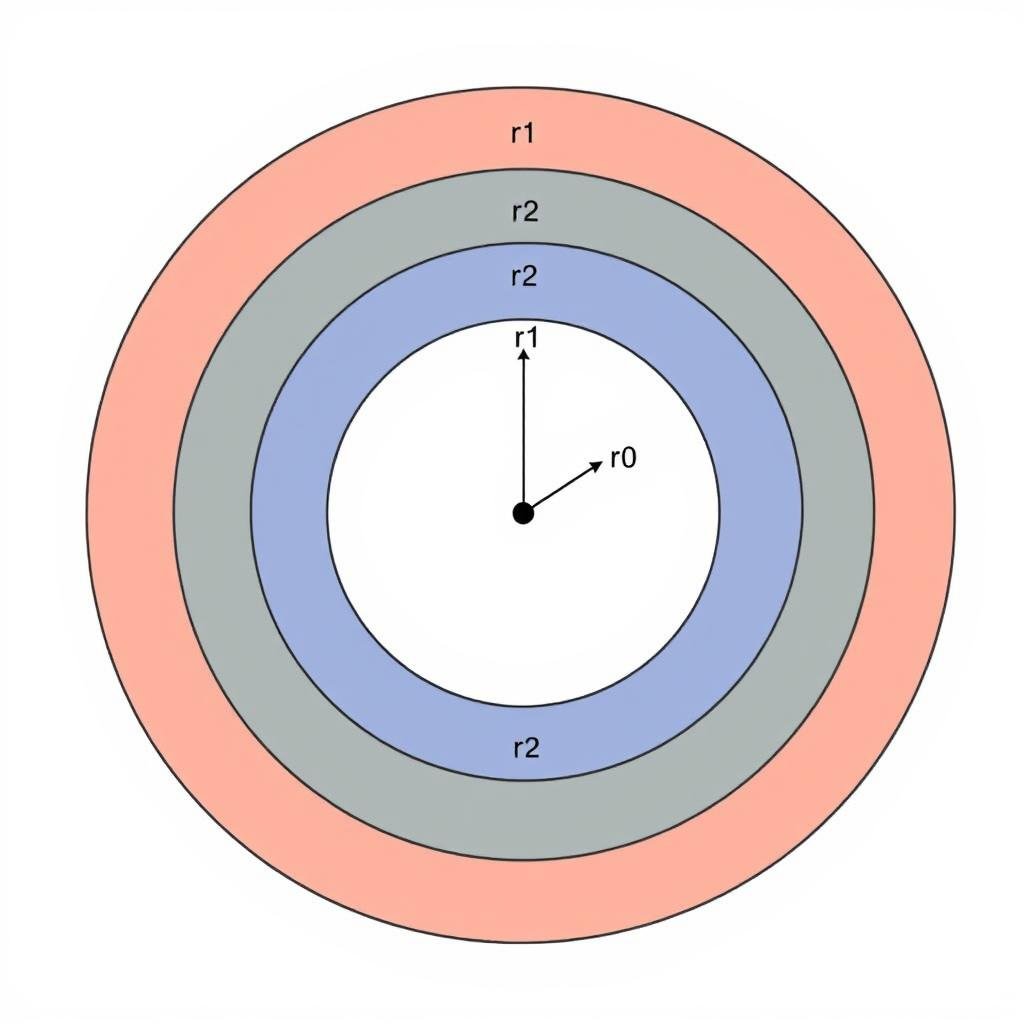
Circles that share the same center point but have different radii. The space between two concentric circles is called an annulus.

Examples in real life include:

• Tree rings
• Archery targets
• Ripples in water
• Vinyl record grooves

Circle Segments & Sectors

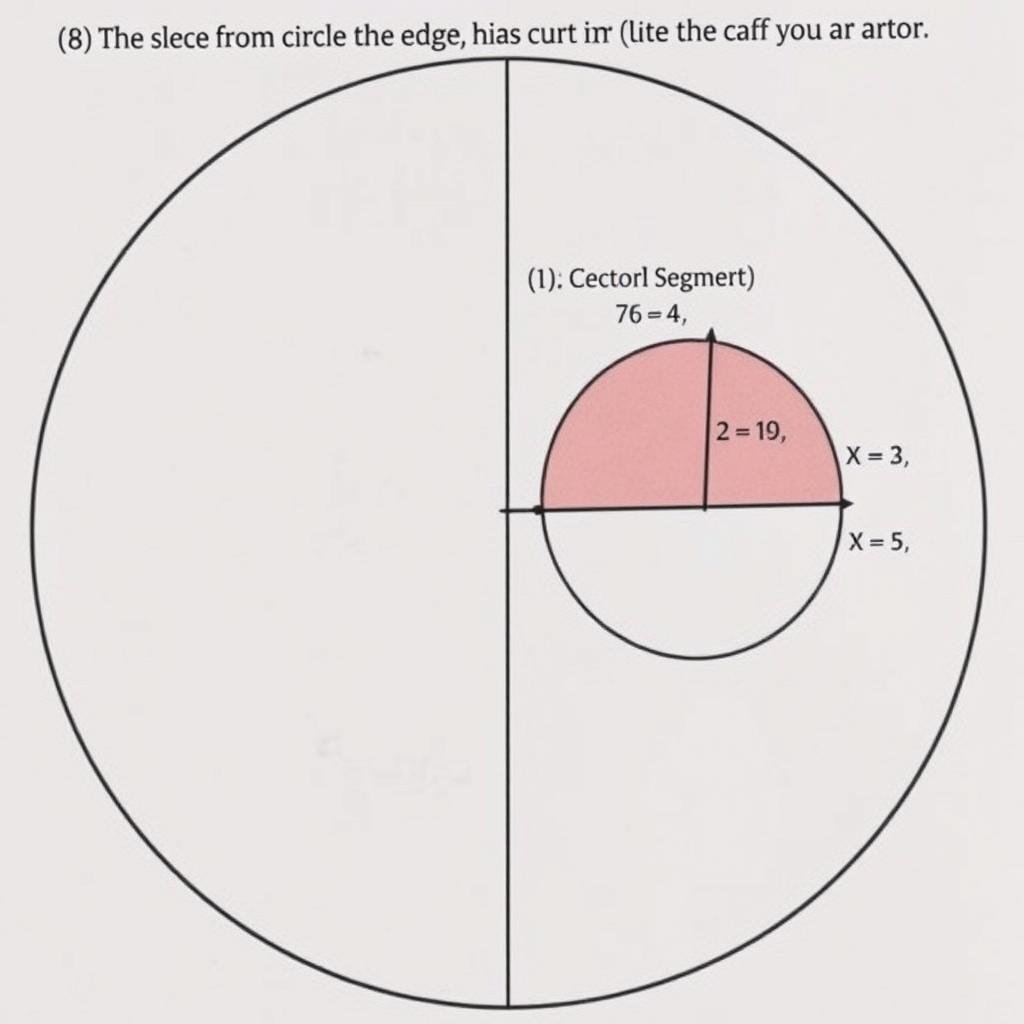
A sector is a "pie slice" of a circle. A segment is the area bounded by an arc and a chord.

For a sector with angle θ (in radians):

• Area = (θ/2)r²
• Arc length = rθ

Why Use Our Circle Calculator?

While understanding how to manually calculate circle measurements is valuable, our Circle Calculator offers several advantages:

Whether you're a student learning geometry, a professional working on designs, or someone tackling a DIY project, our Circle Calculator provides the accuracy and convenience you need for all circle-related calculations.