Use our Compound Interest Calculator to estimate growth on savings or investments. Plan contributions, interest, and future value for smarter financial planning.
Discover the power of compound interest with our easy-to-use calculator. Whether you’re saving for retirement, a home down payment, or your child’s education, understanding how your money grows over time is crucial for achieving your financial goals. Our compound interest calculator helps you visualize your potential returns and make informed decisions about your investments.
What Is Compound Interest?
Compound interest is the interest earned on both your initial investment (principal) and the accumulated interest from previous periods. Unlike simple interest, which is calculated only on the principal amount, compound interest allows your money to grow exponentially over time.
Think of compound interest as a snowball rolling downhill. As it rolls, it collects more snow, becoming larger. The larger it gets, the more snow it collects with each revolution. Similarly, as your investment earns interest, that interest is added to your principal, creating a larger base for earning even more interest in the next period.
“Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn’t, pays it.” – Albert Einstein
The power of compound interest becomes more apparent the longer your money remains invested. Even small differences in interest rates or investment periods can lead to significant differences in your final balance.
The Compound Interest Formula
Understanding the mathematical formula behind compound interest helps you appreciate how your money grows over time. The basic formula for calculating compound interest is:
A = P(1 + r/n)^(nt)
Where:
- A = Final amount (principal + interest)
- P = Principal (initial investment)
- r = Annual interest rate (in decimal form)
- n = Number of times interest is compounded per year
- t = Time period in years
For example, if you invest $1,000 at 5% annual interest compounded monthly for 10 years:
- P = $1,000
- r = 0.05 (5% expressed as a decimal)
- n = 12 (monthly compounding)
- t = 10 years
Plugging these values into the formula: A = $1,000(1 + 0.05/12)^(12×10) = $1,647.01
After 10 years, your $1,000 would grow to $1,647.01, with $647.01 in interest earned.
Skip the Math, Use Our Calculator
Don’t want to work through the formula yourself? Our compound interest calculator does all the calculations for you instantly.
How to Use Our Compound Interest Calculator
Our calculator is designed to be intuitive and easy to use. Follow these simple steps to calculate your potential investment growth:
-
Enter your initial investment amount (principal) in the first field. This is the amount you’re starting with.
-
Input the annual interest rate as a percentage. For example, enter “5” for a 5% interest rate.
-
Select the compounding frequency from the dropdown menu (daily, monthly, quarterly, or annually).
-
Enter the investment time period in years.
-
Add any regular contributions you plan to make and select whether these will be made monthly or annually.
-
Click “Calculate” to see your results.
-
Review the detailed breakdown of your investment growth, including total interest earned and final balance.
-
Use the interactive graph to visualize how your money grows over time.
Our calculator allows you to experiment with different scenarios by adjusting the variables. Try changing the interest rate, contribution amount, or investment period to see how these factors affect your long-term results.
Practical Examples of Compound Interest
Example 1: Retirement Savings
Let’s say you’re 30 years old and want to start saving for retirement at age 65. You have $10,000 to invest initially and can contribute $200 monthly with an expected annual return of 7% compounded monthly.
| Initial Investment | Monthly Contribution | Annual Return | Years | Final Balance | Total Contributions | Total Interest |
| $10,000 | $200 | 7% | 35 | $436,235 | $94,000 | $342,235 |
By consistently investing over 35 years, your $94,000 in total contributions grows to $436,235, with compound interest generating $342,235 – more than 3.6 times what you contributed!
Example 2: Education Fund for a Child
Imagine you want to start a college fund for your newborn child. You invest $5,000 initially and contribute $100 monthly until they turn 18, with an annual return of 6% compounded monthly.
| Initial Investment | Monthly Contribution | Annual Return | Years | Final Balance | Total Contributions | Total Interest |
| $5,000 | $100 | 6% | 18 | $57,434 | $26,600 | $30,834 |
By the time your child is ready for college, your $26,600 in total contributions will have grown to $57,434, with compound interest adding $30,834 to your savings.
Calculate Your Own Scenario
Ready to see how compound interest can help you reach your financial goals? Try our calculator with your own numbers.
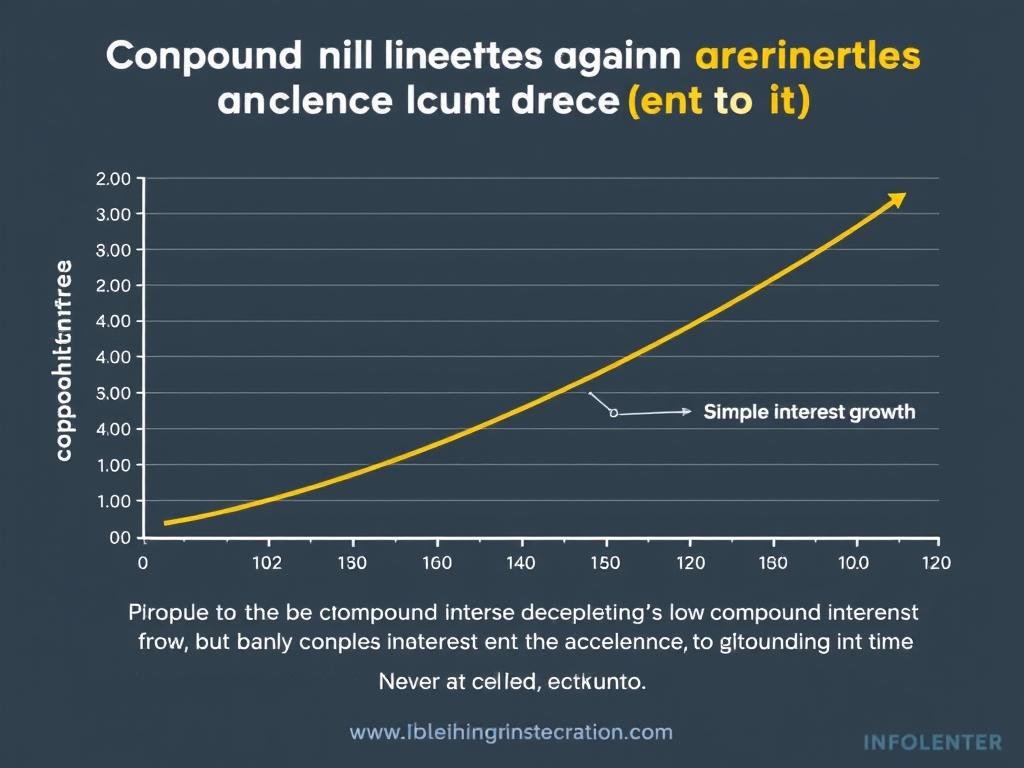
Simple Interest vs. Compound Interest
Understanding the difference between simple and compound interest is crucial for making informed financial decisions.
Simple Interest
Simple interest is calculated only on the initial principal. The interest amount remains the same each period regardless of how long the money is invested.
Formula: I = P × r × t
Where I is the interest, P is principal, r is rate, and t is time.
Example: $1,000 at 5% simple interest for 10 years generates $500 in interest (1000 × 0.05 × 10).
Compound Interest
Compound interest is calculated on the initial principal and on the accumulated interest over previous periods. It grows exponentially over time.
Formula: A = P(1 + r/n)^(nt)
Where A is final amount, P is principal, r is rate, n is compounding frequency, and t is time.
Example: $1,000 at 5% compound interest annually for 10 years generates $628.89 in interest.
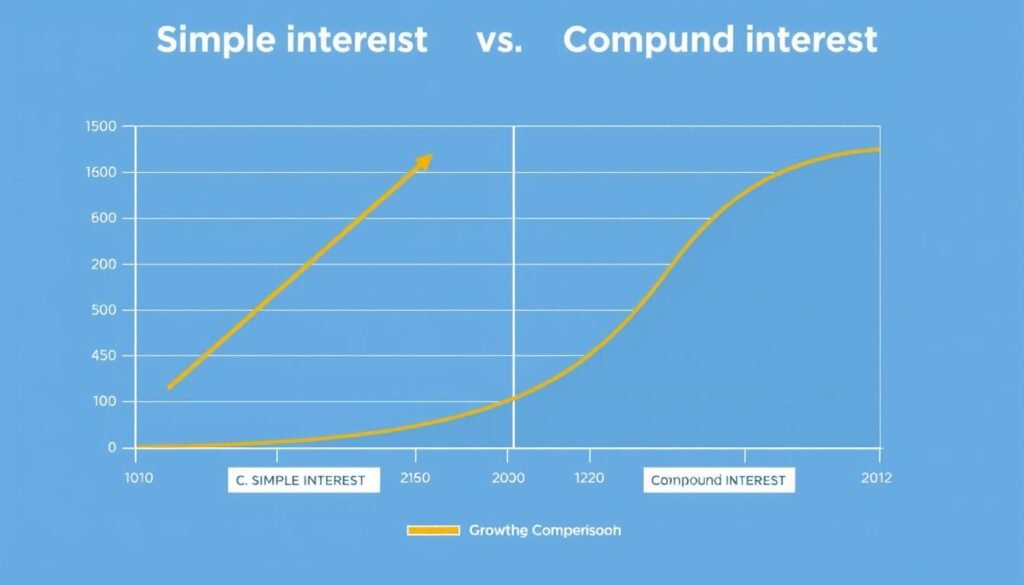
As shown in the comparison, compound interest significantly outperforms simple interest over longer time periods. The difference becomes more dramatic as the investment horizon extends.
Key Factors Affecting Compound Interest Growth
Several factors influence how quickly your money grows through compound interest. Understanding these factors helps you maximize your investment returns.
Initial Principal
The amount you start with affects your overall growth. A larger initial investment provides a bigger base for compound interest to work with.
However, don’t be discouraged if you can only start small. Regular contributions over time can still lead to significant growth.
Interest Rate
Even small differences in interest rates can dramatically impact your final balance over long periods. A 1-2% increase in your rate of return can result in tens of thousands of additional dollars over decades.
This is why it’s important to shop around for the best rates for savings accounts or consider higher-return investments for long-term goals.
Time Period
Time is perhaps the most powerful factor in compound interest. The longer your money has to grow, the more dramatic the compounding effect becomes.
Starting early, even with smaller amounts, often outperforms starting later with larger amounts due to the exponential nature of compound growth.
Compounding Frequency
How often interest is calculated and added to your principal affects your returns. More frequent compounding (daily vs. monthly vs. annually) results in higher returns.
For example, daily compounding will generate more interest than annual compounding at the same stated interest rate.
Regular Contributions
Adding regular contributions to your investment accelerates growth significantly. Each new contribution begins its own compound interest journey.
Consistent contributions, even small ones, can dramatically increase your final balance compared to a one-time investment.
Taxes and Inflation
Taxes on investment earnings and inflation can reduce your effective returns. Consider tax-advantaged accounts and adjust for inflation when planning long-term investments.
An investment growing at 7% in an environment with 3% inflation has a real return of approximately 4%.
Advanced Compound Interest Concepts
The Rule of 72
The Rule of 72 is a simple way to estimate how long it will take for your investment to double in value. Simply divide 72 by your annual interest rate (as a whole number) to get the approximate number of years.
| Interest Rate | Years to Double (Rule of 72) | Actual Years to Double |
| 4% | 18.0 | 17.7 |
| 6% | 12.0 | 11.9 |
| 8% | 9.0 | 9.0 |
| 10% | 7.2 | 7.3 |
| 12% | 6.0 | 6.1 |
For example, at a 6% annual return, your money will double in approximately 12 years (72 ÷ 6 = 12).
Continuous Compounding
Continuous compounding represents the mathematical limit of compound interest, where interest is calculated and added to the principal continuously. The formula for continuous compounding is:
A = Pe^(rt)
Where:
- A = Final amount
- P = Principal
- e = Mathematical constant (approximately 2.71828)
- r = Annual interest rate (in decimal form)
- t = Time in years
Continuous compounding provides the highest possible return for a given interest rate, though the difference between daily compounding and continuous compounding is minimal in practice.
The Impact of Inflation
When planning long-term investments, it’s important to account for inflation, which erodes purchasing power over time. To calculate your real rate of return, subtract the inflation rate from your nominal interest rate.
For example, if your investment earns 7% annually but inflation is 3%, your real rate of return is approximately 4%. Our calculator can help you factor in inflation to get a more accurate picture of your investment’s future purchasing power.
Frequently Asked Questions
What’s the difference between APR and APY?
APR (Annual Percentage Rate) is the stated interest rate without accounting for compounding. APY (Annual Percentage Yield) includes the effect of compounding and represents the actual return you’ll receive over a year. For example, a 5% APR compounded monthly would result in a 5.12% APY.
How does compound interest work against me with debt?
With debt, compound interest works in the lender’s favor. If you don’t pay off your balance, interest is added to your principal, and future interest calculations include this higher amount. This is particularly problematic with high-interest debt like credit cards, where interest can compound daily, causing your debt to grow rapidly if only minimum payments are made.
Is it better to make a lump sum investment or regular contributions?
Mathematically, investing a lump sum earlier will generally outperform the same amount spread over time, due to the longer compounding period. However, regular contributions have advantages too: they help average out market fluctuations (dollar-cost averaging) and may be more practical for most people’s budgets. Our calculator can help you compare both approaches.
How do taxes affect compound interest?
Taxes can significantly impact your investment returns. In taxable accounts, you pay taxes on interest, dividends, and capital gains as they occur, reducing the amount that compounds. Tax-advantaged accounts like IRAs and 401(k)s allow your investments to grow tax-deferred or tax-free, maximizing the power of compound interest.
What investments offer compound interest?
Many investments benefit from compound growth, including savings accounts, certificates of deposit (CDs), bonds, dividend-paying stocks (when dividends are reinvested), and mutual funds. The rate of return varies significantly between these options, with generally higher returns associated with higher risk investments.
Have More Questions?
Our compound interest calculator can help you answer specific questions about your financial situation.
Explore Related Financial Calculators
Enhance your financial planning with these additional calculators from CalculatorHunt.com:
Savings Calculator
Plan your savings strategy and see how regular deposits can help you reach your financial goals.
Retirement Calculator
Determine how much you need to save for a comfortable retirement and track your progress.
Loan Calculator
Calculate monthly payments, total interest, and amortization schedules for various loan types.
Harness the Power of Compound Interest Today
Compound interest is one of the most powerful forces in finance, capable of transforming modest savings into substantial wealth over time. By understanding how it works and using our calculator to run different scenarios, you can make more informed decisions about your savings and investments.
Remember that time is your greatest ally when it comes to compound interest. The sooner you start saving and investing, the more you’ll benefit from the exponential growth that compounding provides. Even small amounts, consistently invested over long periods, can grow into significant sums.
Start Growing Your Money Today
Use our compound interest calculator to see how your savings can grow over time and take the first step toward achieving your financial goals.