Density is a fundamental physical property that helps us understand how matter is distributed in objects and substances. Whether you’re a student working on physics homework, an engineer designing materials, or simply curious about the world around you, understanding density is essential. This comprehensive guide will walk you through everything you need to know about density calculations, from the basic formula to real-world applications.
What is Density?

Density is defined as the mass of an object divided by its volume. It tells us how tightly packed the matter is within a substance. The standard unit for density is kilograms per cubic meter (kg/m³), though other units like grams per cubic centimeter (g/cm³) are also commonly used.
Think of density as a measure of how “heavy” an object feels for its size. A small piece of lead feels much heavier than a large piece of foam because lead has a much higher density. This fundamental property helps explain why some objects float while others sink, and it’s crucial in fields ranging from engineering to geology.
Need Quick Density Calculations?
Skip the manual calculations and get instant results with our easy-to-use online tool.
The Density Formula Explained
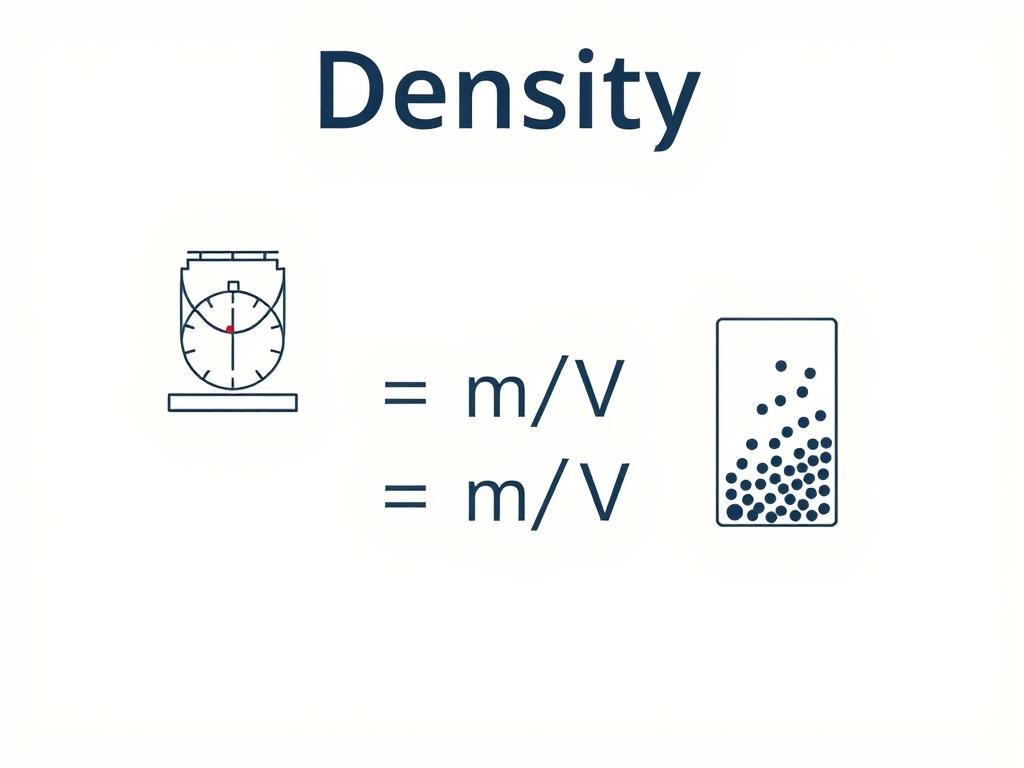
The basic density formula is remarkably simple, yet powerful:
Density (ρ) = Mass (m) / Volume (V)
This formula can be rearranged to find any of the three variables:
- To find mass: Mass (m) = Density (ρ) × Volume (V)
- To find volume: Volume (V) = Mass (m) / Density (ρ)
Understanding this relationship is crucial for solving density problems. For example, if you know an object has a mass of 300 grams and a volume of 100 cubic centimeters, you can calculate its density as 3 g/cm³.
Common Units for Density Calculations
| Measurement | Common Units | Conversion Factors |
| Mass | Kilograms (kg), Grams (g), Pounds (lb) | 1 kg = 1000 g = 2.205 lb |
| Volume | Cubic meters (m³), Cubic centimeters (cm³), Liters (L) | 1 m³ = 1,000,000 cm³ = 1000 L |
| Density | kg/m³, g/cm³, lb/ft³ | 1 g/cm³ = 1000 kg/m³ = 62.4 lb/ft³ |
When performing density calculations, it’s essential to use consistent units. If you’re working with mass in grams and volume in cubic centimeters, your density will be in g/cm³. If you need to convert to different units, use the conversion factors in the table above.
How to Calculate Density: Step-by-Step Guide
Calculating density is straightforward when you follow these steps:
- Measure the mass of the object using a scale or balance.
- Determine the volume of the object (methods vary depending on the object’s shape).
- Ensure both measurements are in compatible units.
- Divide the mass by the volume using the density formula.
- Express the result in appropriate density units.
Methods for Measuring Volume
For Regular Shapes:
- Cube or rectangular prism: Volume = length × width × height
- Sphere: Volume = (4/3) × π × radius³
- Cylinder: Volume = π × radius² × height
For Irregular Shapes:
- Water displacement method: Measure the volume of water displaced when the object is submerged
- For liquids: Use a graduated cylinder or measuring cup
- For gases: Use specialized equipment like a gas syringe
Ready to Calculate Density?
Our online calculator handles all types of density problems instantly.
Practical Density Calculation Examples
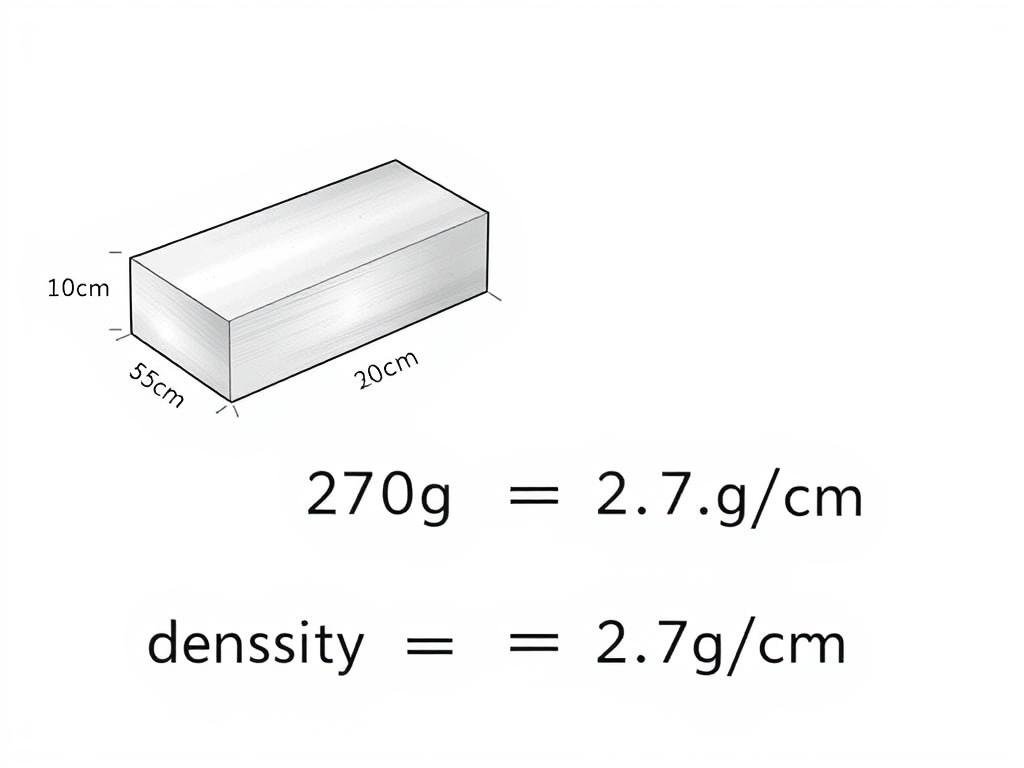
Example 1: Finding Density of a Solid Block
Problem: A rectangular aluminum block measures 10 cm × 5 cm × 2 cm and has a mass of 270 grams. Calculate its density.
Solution:
- Calculate the volume: V = 10 cm × 5 cm × 2 cm = 100 cm³
- Use the density formula: ρ = m/V = 270 g ÷ 100 cm³ = 2.7 g/cm³
- The density of the aluminum block is 2.7 g/cm³ or 2,700 kg/m³
Example 2: Finding Mass Using Density
Problem: A liquid has a density of 0.8 g/cm³. What is the mass of 250 cm³ of this liquid?
Solution:
- Rearrange the density formula to find mass: m = ρ × V
- Substitute the values: m = 0.8 g/cm³ × 250 cm³ = 200 g
- The mass of the liquid is 200 grams
Example 3: Finding Volume Using Density
Problem: An iron object with a mass of 3.93 kg has a density of 7,860 kg/m³. What is its volume?
Solution:
- Rearrange the density formula to find volume: V = m ÷ ρ
- Substitute the values: V = 3.93 kg ÷ 7,860 kg/m³ = 0.0005 m³
- Convert to cm³: 0.0005 m³ = 500 cm³
- The volume of the iron object is 500 cm³
Struggling with Density Problems?
Our calculator can handle all these examples and more with just a few clicks.
Factors Affecting Density
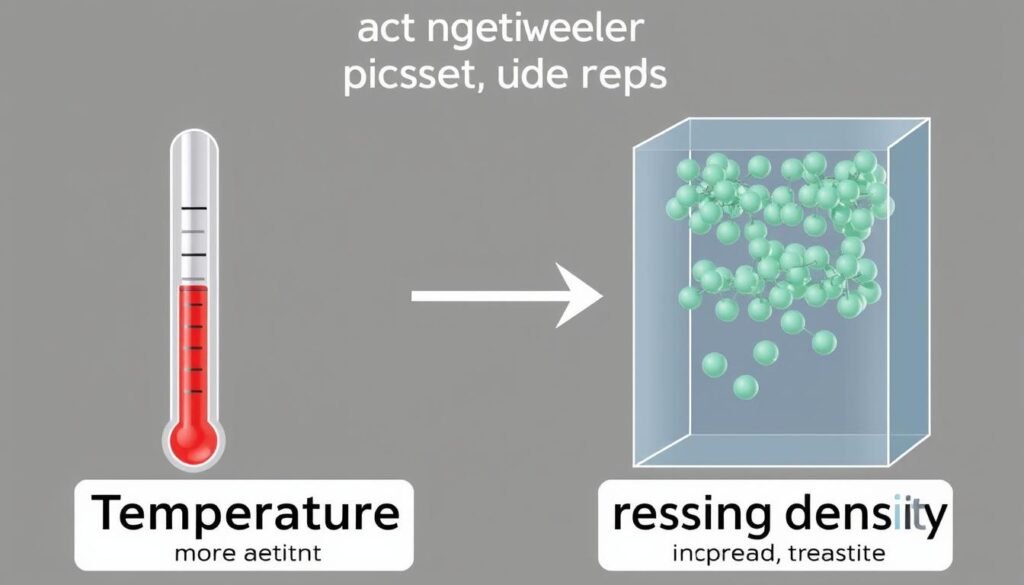
Temperature Effects
For most substances, density decreases as temperature increases. This happens because higher temperatures cause molecules to move faster and spread out, increasing the volume while the mass remains constant.
Water is a notable exception between 0°C and 4°C. Water reaches its maximum density at 4°C and becomes less dense both above and below this temperature. This unusual property explains why ice floats on water and why lakes freeze from the top down.
Pressure Effects
Increasing pressure typically increases density, especially in gases and liquids. Under higher pressure, molecules are forced closer together, decreasing volume while mass remains constant.
This relationship is particularly important in meteorology, oceanography, and engineering applications where pressure variations significantly impact material properties.
Densities of Common Materials
| Material | Density (g/cm³) | Density (kg/m³) | Category |
| Air (at sea level) | 0.0012 | 1.2 | Gas |
| Water (4°C) | 1.0 | 1,000 | Liquid |
| Ice | 0.92 | 920 | Solid |
| Wood (Oak) | 0.7-0.9 | 700-900 | Solid |
| Aluminum | 2.7 | 2,700 | Metal |
| Iron | 7.87 | 7,870 | Metal |
| Gold | 19.3 | 19,300 | Metal |
| Mercury | 13.6 | 13,600 | Liquid Metal |

Understanding the densities of common materials helps explain everyday phenomena. For instance, ice floats in water because its density (0.92 g/cm³) is less than that of liquid water (1.0 g/cm³). Similarly, a wooden boat floats because its average density (including the hollow spaces) is less than water’s density.
Real-World Applications of Density
Scientific Research

Scientists use density measurements to identify unknown substances, verify material purity, and study material properties under different conditions.
Engineering
Engineers consider density when selecting materials for construction, designing floating vessels, and developing new alloys with specific properties.
Everyday Life

From cooking (where recipes might specify volume but ingredients are measured by weight) to determining if your car battery fluid needs replacement, density calculations appear in many daily activities.

Frequently Asked Questions About Density
Why is density important?
Density is important because it helps us understand how materials behave under different conditions. It explains why some objects float while others sink, helps identify unknown substances, and is crucial for designing everything from ships to aircraft.
Can density be negative?
No, density cannot be negative in classical physics. Since both mass and volume are always positive values, their ratio (density) must also be positive. However, in certain specialized contexts like astrophysics, the concept of “negative density” might be used to describe exotic theoretical phenomena.
How do I find the density of an irregular object?
For irregular objects, measure the mass using a scale, then determine the volume using water displacement. Place a known volume of water in a graduated cylinder, submerge the object completely, and measure the increase in water level. The difference is the object’s volume. Then divide the mass by this volume.
Why does ice float on water?
Ice floats on water because it’s less dense than liquid water. When water freezes, the molecules arrange themselves in a crystalline structure that takes up more space than when in liquid form, making ice about 9% less dense than liquid water.
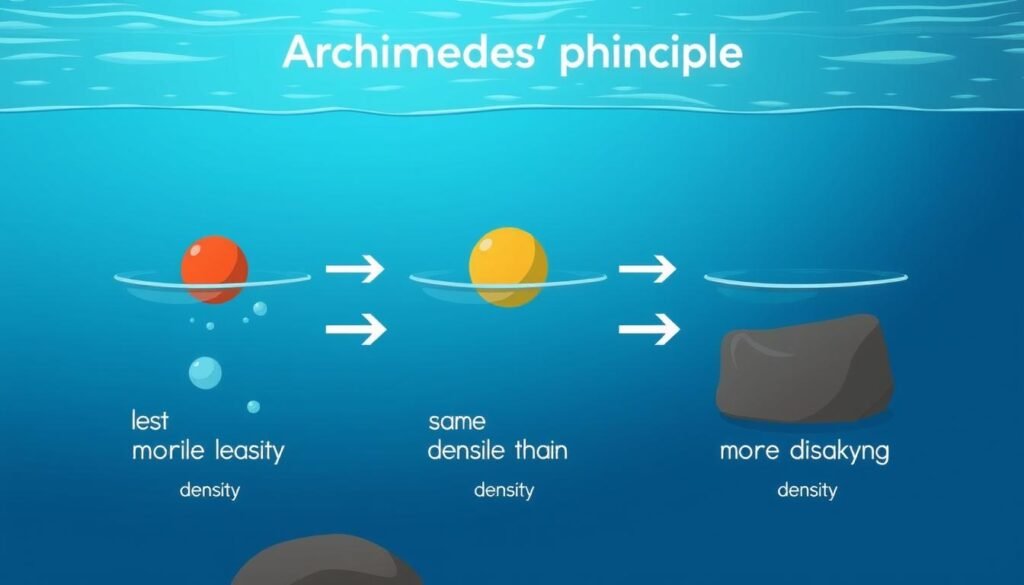
How does density affect buoyancy?
Buoyancy is directly related to density. Archimedes’ principle states that an object immersed in a fluid experiences an upward force equal to the weight of the fluid it displaces. If an object’s density is less than the fluid’s density, it will float; if greater, it will sink.
Conclusion: Mastering Density Calculations
Understanding density and how to calculate it is essential for students, professionals, and curious minds alike. From determining if an object will float to identifying unknown materials, density calculations have countless practical applications in science, engineering, and everyday life.
By mastering the simple formula ρ = m/V and understanding how to measure mass and volume accurately, you can solve a wide range of density-related problems. Remember that density can be affected by temperature and pressure, so consider these factors when making precise calculations.
Ready to Simplify Your Density Calculations?
Our free online Density Calculator handles all the math for you, providing instant, accurate results for any density problem.
Whether you’re a student working on physics homework, a professional needing precise measurements, or simply curious about the physical properties of materials, our Density Calculator is the perfect tool to save time and ensure accuracy in all your density-related calculations.