Distance Calculator helps you find the distance between two points using coordinates, addresses, or maps. Fast, accurate, and easy to use online tool.
Distance Calculator
Understanding how to calculate distance between points is essential for various applications, from navigation and travel planning to scientific research and engineering. Whether you need to find the shortest path between two locations, measure the distance on a map, or calculate spatial relationships in mathematics, having the right distance calculation method makes all the difference. This comprehensive guide explores everything you need to know about distance calculation, its methods, applications, and benefits.

What is Distance Calculation?
Distance calculation is the process of determining the spatial separation between two or more points in various coordinate systems. This fundamental concept applies to numerous fields, from everyday navigation to complex scientific applications. The method used to calculate distance depends on the context and the coordinate system in which the points exist.
In its simplest form, distance calculation involves measuring the length of the path connecting two points. However, this seemingly straightforward concept becomes more complex when considering different types of spaces, coordinate systems, and real-world constraints. For instance, the distance between two cities might be measured as a straight line (as the crow flies) or along road networks (driving distance).
The accuracy of distance calculations is crucial for many applications. Even small errors can lead to significant problems in navigation, logistics planning, or scientific research. That’s why understanding the appropriate calculation method for your specific needs is essential for obtaining reliable results.
Need Accurate Distance Measurements?
Our distance calculator provides precise measurements using various calculation methods tailored to your specific needs.
Distance Calculation Methods
Different contexts require different approaches to calculating distance. Here are the most common distance calculation methods used across various applications:
Euclidean Distance
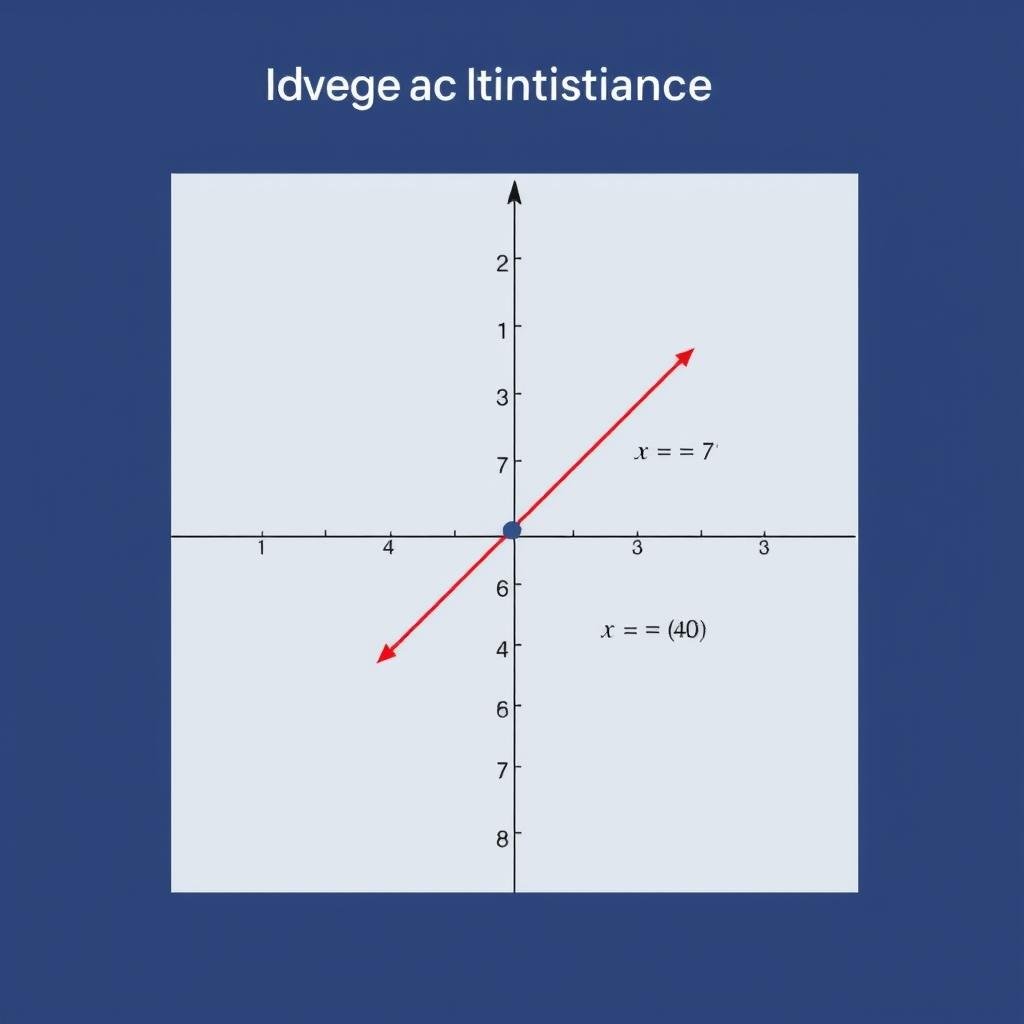
The most familiar method, Euclidean distance measures the straight-line or “as the crow flies” distance between two points. In a two-dimensional plane, it’s calculated using the Pythagorean theorem:
d = √[(x₂ – x₁)² + (y₂ – y₁)²]
In three-dimensional space, the formula extends to include the z-coordinate:
d = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]
Manhattan Distance
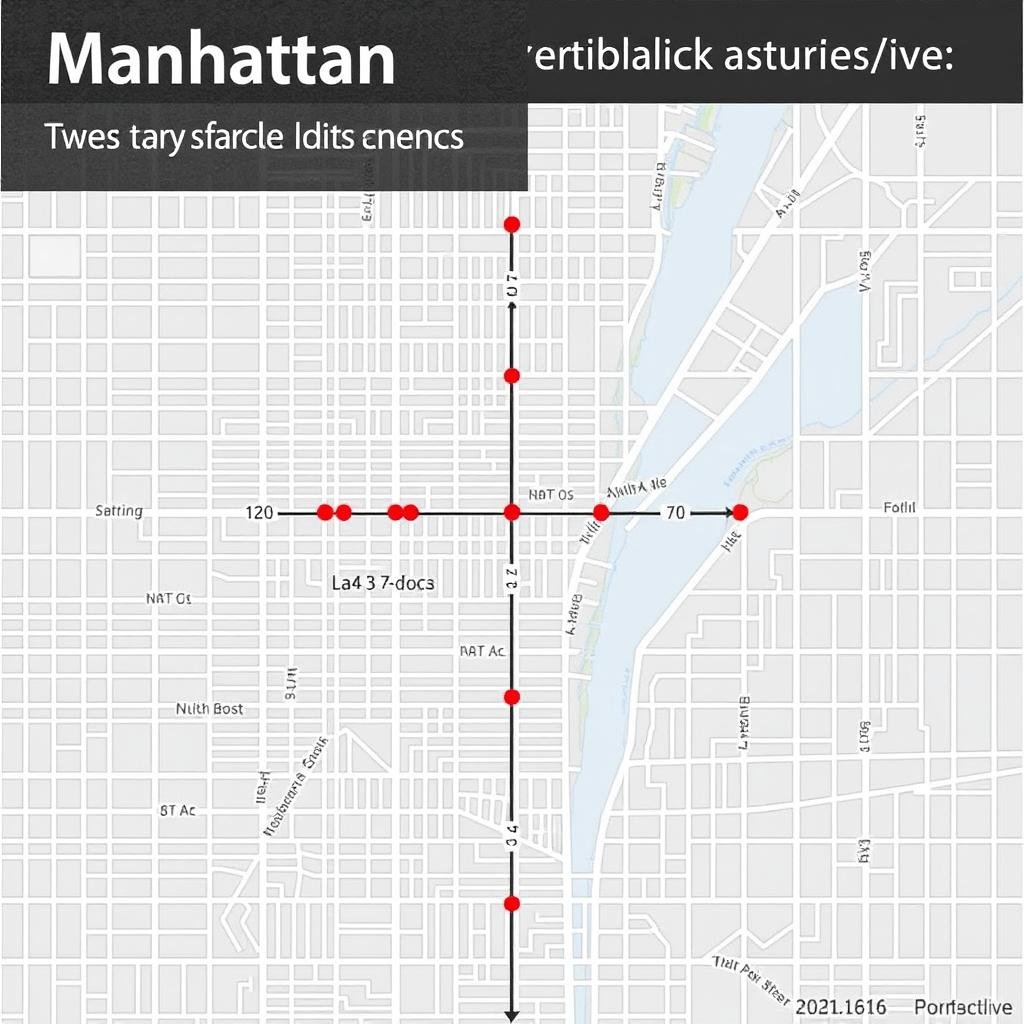
Also known as taxicab or city block distance, Manhattan distance calculates the sum of absolute differences between coordinates. It’s named after the grid layout of Manhattan streets:
d = |x₂ – x₁| + |y₂ – y₁|
This method is particularly useful in grid-based systems or when movement is restricted to horizontal and vertical paths, such as in city navigation or circuit design.
Great Circle Distance
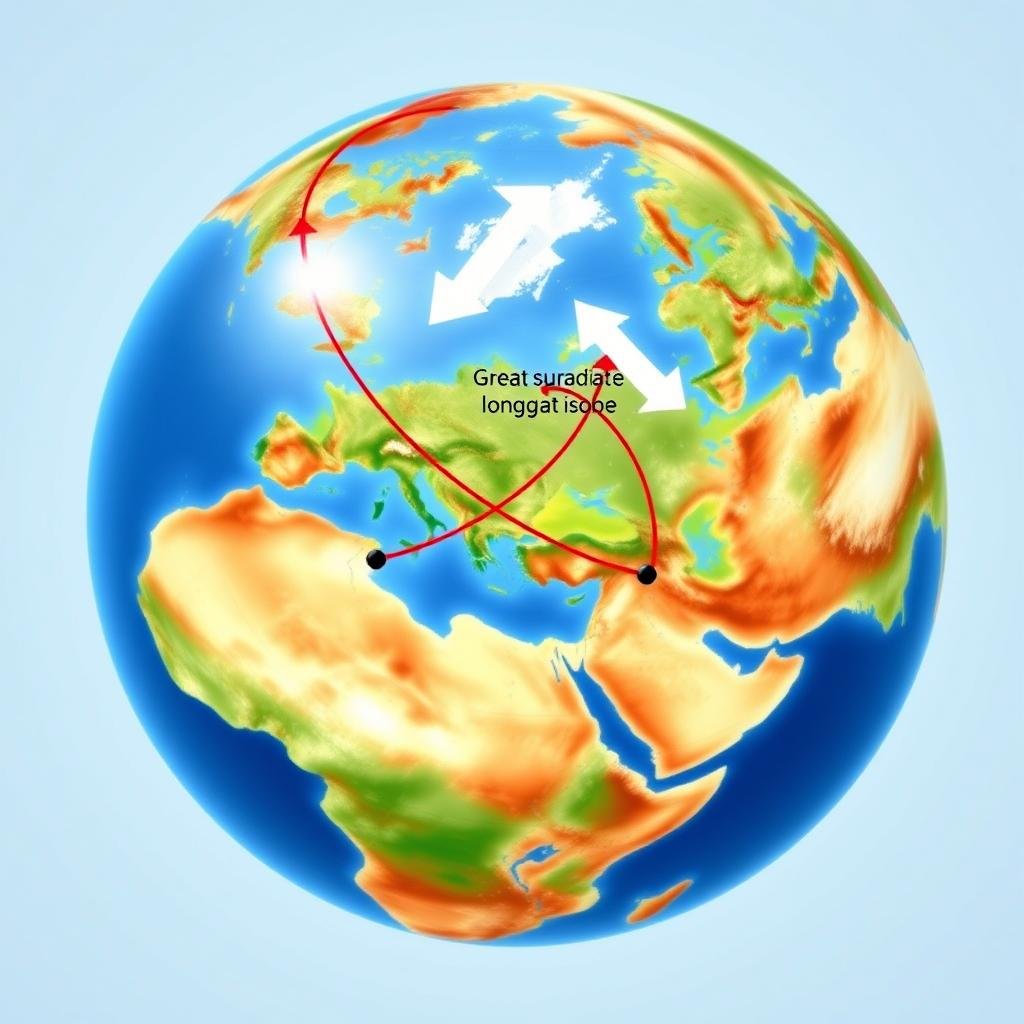
When calculating distances on Earth’s surface, the great circle distance provides the shortest path between two points on a sphere. It’s calculated using the Haversine formula:
d = 2r × arcsin(√[sin²((φ₂ – φ₁)/2) + cos(φ₁) × cos(φ₂) × sin²((λ₂ – λ₁)/2)])
Where r is Earth’s radius, φ represents latitude, and λ represents longitude (in radians). This method is essential for aviation, maritime navigation, and global distance calculations.
Choosing the right distance calculation method depends on your specific application. For everyday mapping and navigation on Earth’s surface, the great circle distance is most appropriate. For mathematical or engineering applications in flat spaces, Euclidean distance is typically used. When movement is restricted to grid patterns, Manhattan distance provides more realistic measurements.
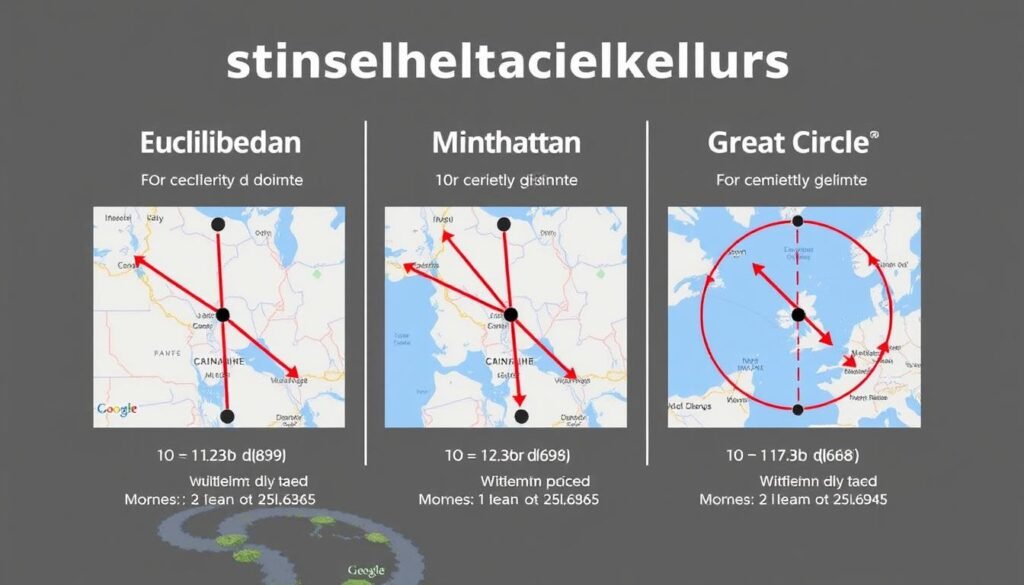
Comparison of different distance calculation methods between the same two points
Real-World Applications of Distance Calculation
Distance calculation is fundamental to numerous fields and everyday activities. Understanding how these calculations are applied can help you appreciate their importance and choose the right method for your needs.
Navigation and Travel
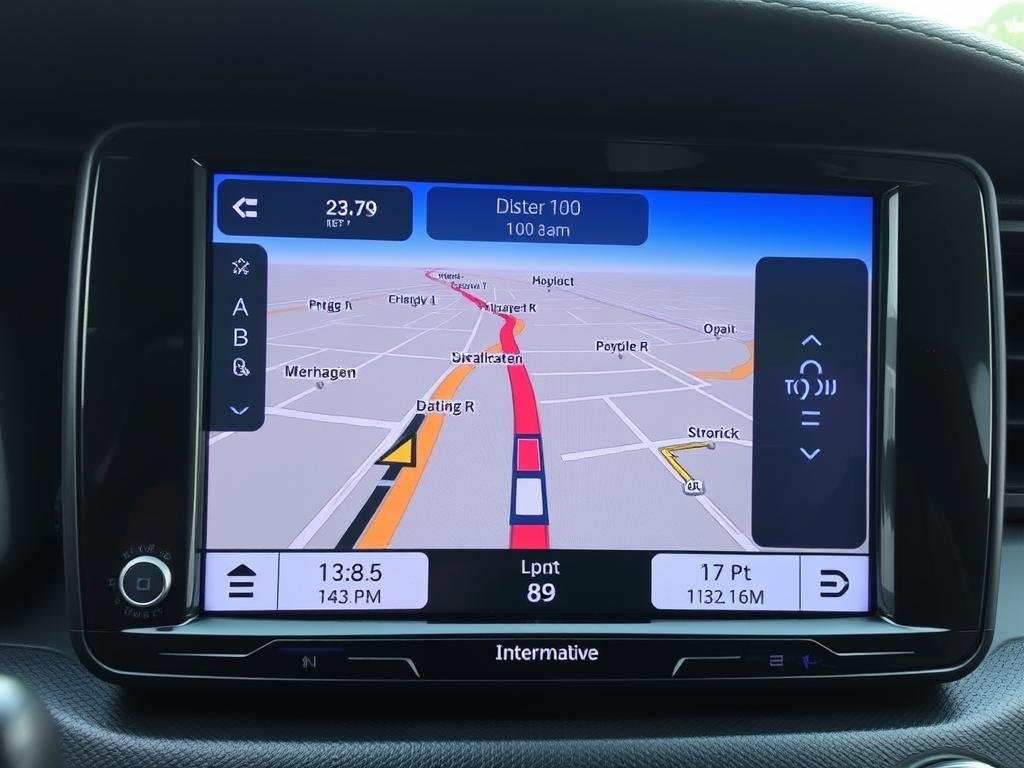
Distance calculation forms the backbone of navigation systems, from GPS devices to mapping applications. These tools use various distance algorithms to:
- Determine the shortest route between locations
- Estimate travel time based on distance and speed
- Calculate fuel consumption for journeys
- Provide alternative routes with distance comparisons
For aviation and maritime navigation, great circle distance calculations are essential for plotting efficient courses across the globe.
Logistics and Supply Chain
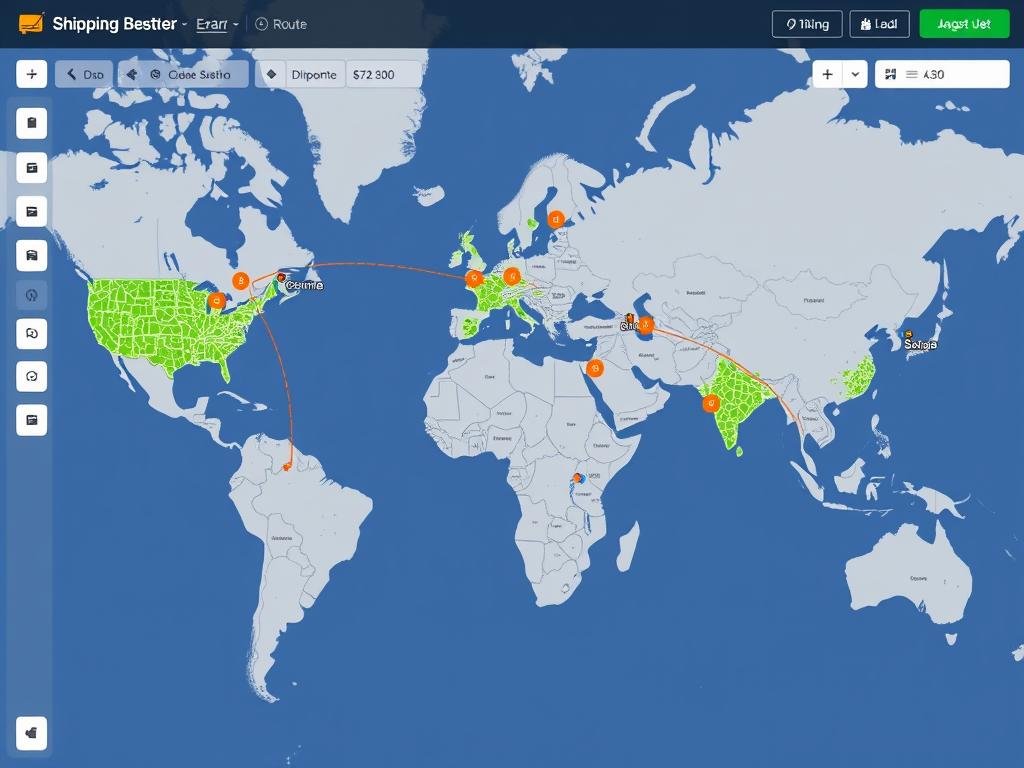
In logistics and supply chain management, accurate distance calculations help optimize:
- Delivery routes for maximum efficiency
- Warehouse placement to minimize transportation costs
- Shipping time estimates for customer communication
- Fuel and resource allocation for transportation
Companies use sophisticated distance algorithms to reduce costs and improve service by finding the most efficient routes for goods movement.
Planning a Trip or Route?
Calculate distances accurately to better plan your journey, estimate travel time, and optimize your route.
Science and Research
Scientists use distance calculations in various disciplines:
- Astronomy: Measuring distances between celestial bodies
- Ecology: Analyzing animal movement patterns
- Geology: Mapping fault lines and geological features
- Meteorology: Tracking weather systems and predicting movements
Urban Planning
City planners rely on distance calculations for:
- Optimizing public transportation routes
- Planning emergency service coverage areas
- Designing walkable neighborhoods
- Determining school district boundaries
Sports and Fitness
Distance measurement is crucial in sports for:
- Tracking running, cycling, or swimming distances
- Designing race courses of specific lengths
- Analyzing player movement in team sports
- Setting up field dimensions for competitions
Common Distance Units and Conversions
Understanding different distance units and how to convert between them is essential for accurate distance calculation. Here are the most commonly used distance units and their relationships:
| Unit | Symbol | Metric Equivalent | Imperial Equivalent | Common Usage |
| Millimeter | mm | 0.001 m | 0.03937 inches | Small measurements, precision engineering |
| Centimeter | cm | 0.01 m | 0.3937 inches | Everyday small measurements |
| Meter | m | 1 m | 3.28084 feet | Standard metric unit, room dimensions |
| Kilometer | km | 1,000 m | 0.621371 miles | Road distances, city planning |
| Inch | in | 0.0254 m | 1/12 foot | Small measurements in US/UK |
| Foot | ft | 0.3048 m | 12 inches | Height, room dimensions in US |
| Mile | mi | 1,609.34 m | 5,280 feet | Road distances in US/UK |
| Nautical Mile | nmi | 1,852 m | 1.15078 miles | Maritime and aviation navigation |
Converting between distance units is a common requirement when working with different systems or applications. For example, to convert kilometers to miles, multiply by 0.621371. To convert feet to meters, multiply by 0.3048.
Modern distance calculators offer seamless unit conversion capabilities
Need to Convert Between Distance Units?
Our distance calculator handles all unit conversions automatically, saving you time and preventing conversion errors.
Benefits of Using an Online Distance Calculator
While manual distance calculations are possible, online distance calculators offer numerous advantages that make them the preferred choice for most applications. Here’s why you should consider using an online distance calculator:
Advantages of Online Distance Calculators
- Accuracy: Eliminates human calculation errors, especially for complex formulas like great circle distance
- Speed: Instantly calculates distances that would take significant time manually
- Multiple Methods: Easily switch between Euclidean, Manhattan, and great circle calculations
- Unit Conversion: Automatically converts between different measurement units
- Visual Representation: Many calculators show the distance on maps or graphs for better understanding
- Batch Processing: Calculate multiple distances simultaneously for route planning
- Integration: Many calculators work with mapping services for real-world applications
- Accessibility: Available on any device with internet access, no specialized knowledge required

Whether you’re planning a road trip, analyzing geographic data, or solving a mathematical problem, an online distance calculator streamlines the process and ensures reliable results. The ability to quickly switch between different calculation methods and measurement units makes these tools invaluable for both casual and professional users.
Experience These Benefits Yourself
Try our comprehensive distance calculator and see how it simplifies your distance measurement needs.
How Distance Calculation Works: Behind the Scenes
Understanding the mechanics behind distance calculation can help you choose the right method for your specific needs. Here’s a step-by-step breakdown of how different distance calculation methods work:
Euclidean Distance Calculation
- Identify the coordinates of both points (x₁, y₁) and (x₂, y₂)
- Calculate the difference between x-coordinates: (x₂ – x₁)
- Calculate the difference between y-coordinates: (y₂ – y₁)
- Square both differences: (x₂ – x₁)² and (y₂ – y₁)²
- Add the squared differences: (x₂ – x₁)² + (y₂ – y₁)²
- Take the square root of the sum: √[(x₂ – x₁)² + (y₂ – y₁)²]
The result is the straight-line distance between the two points. For 3D calculations, simply add the z-coordinate difference squared to the sum before taking the square root.
Great Circle Distance Calculation
- Convert latitude and longitude from degrees to radians
- Calculate the difference in longitude: Δλ = λ₂ – λ₁
- Apply the Haversine formula: a = sin²(Δφ/2) + cos(φ₁) × cos(φ₂) × sin²(Δλ/2)
- Calculate the central angle: c = 2 × atan2(√a, √(1-a))
- Multiply by Earth’s radius (R ≈ 6,371 km): d = R × c
This calculation accounts for Earth’s curvature, providing the shortest distance along the surface between two points. For even greater accuracy, ellipsoidal models like WGS84 can be used instead of a perfect sphere.

Modern distance calculators handle these complex calculations instantly, often incorporating additional features like:
- Elevation data for more accurate terrestrial distance measurements
- Road network integration to calculate driving distances rather than straight-line distances
- Multiple waypoint support for calculating cumulative distances along a route
- Real-time updates based on traffic or weather conditions for navigation applications
By understanding these calculation methods, you can better interpret the results and choose the most appropriate approach for your specific distance measurement needs.
Frequently Asked Questions About Distance Calculation
What is the difference between Euclidean and Manhattan distance?
Euclidean distance measures the straight-line or “as the crow flies” distance between two points, calculated using the Pythagorean theorem. Manhattan distance (also called taxicab or city block distance) measures the sum of the absolute differences of their coordinates, representing the distance traveled along grid lines. Euclidean distance is typically shorter than Manhattan distance, except when points are aligned horizontally or vertically.
Why is great circle distance used for global navigation?
Great circle distance is used for global navigation because it represents the shortest path between two points on the surface of a sphere (like Earth). Unlike flat-map projections that distort distances, great circle calculations account for Earth’s curvature, providing the most efficient route for ships and aircraft. This is why long-distance flights often appear curved when drawn on a flat map but are actually following the shortest possible path.
How accurate are online distance calculators?
The accuracy of online distance calculators depends on several factors: the calculation method used, the quality of input data, and whether they account for real-world factors. For mathematical calculations in 2D or 3D space, they can be extremely accurate. For Earth-based calculations, most quality calculators are accurate within 0.1-0.5% when using great circle methods. Calculators that incorporate elevation data and use ellipsoidal Earth models (rather than spherical) provide the highest accuracy for terrestrial measurements.
Can distance calculators account for road routes?
Yes, many advanced distance calculators can calculate road distances by integrating with mapping services and road network databases. These calculators determine the shortest or fastest route along existing roads rather than measuring straight-line distances. They may also account for factors like one-way streets, traffic conditions, and road closures. However, these calculations are more complex and may require more specialized tools than basic distance calculators.
What units should I use for distance calculation?
The best units to use depend on your application and regional standards. For everyday measurements in the United States, miles are commonly used for long distances and feet for shorter ones. Most other countries use kilometers and meters (metric system). For scientific applications, meters are the standard SI unit. For aviation and maritime navigation, nautical miles are preferred. Good distance calculators allow you to input coordinates in one unit system and display results in another, eliminating the need for manual conversion.
Start Calculating Distances Accurately Today
Distance calculation is a fundamental concept with applications spanning from everyday navigation to complex scientific research. By understanding the different calculation methods and their appropriate uses, you can ensure accurate and meaningful distance measurements for any purpose.
Whether you’re planning a trip, analyzing geographic data, or solving mathematical problems, having access to a reliable distance calculator streamlines the process and eliminates potential errors. Our comprehensive distance calculator offers multiple calculation methods, unit conversions, and intuitive visualization to meet all your distance measurement needs.
Ready to Calculate Distances with Precision?
Our easy-to-use distance calculator provides accurate measurements using the most appropriate methods for your specific needs.
For additional measurement tools and calculators, explore our related resources on area calculation, coordinate conversion, and route optimization. Accurate distance calculation is just the beginning of what our suite of measurement tools can offer.