Factors are fundamental building blocks in mathematics that help us understand the relationships between numbers. A factor calculator simplifies the process of finding all possible factors of a number, determining greatest common factors (GCF), and performing prime factorization. Whether you’re a student tackling algebra problems, a teacher preparing math lessons, or simply someone looking to enhance their mathematical skills, understanding factors and having access to a reliable factor calculator can make complex calculations straightforward and efficient.
What Are Factors and Why Are They Important?

Factors of 12 represented as rectangular arrays
In mathematics, factors are numbers that divide another number evenly, with no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Understanding factors is crucial for various mathematical operations, including:
- Simplifying fractions
- Finding common denominators
- Solving algebraic equations
- Working with polynomials
- Understanding number properties
A factor calculator automates the process of finding all factors of a given number, saving time and reducing the possibility of errors in calculations.
Need to Find Factors Quickly?
Our Factor Calculator can instantly determine all factors of any positive integer, helping you solve mathematical problems efficiently.
How to Find Factors Manually
Before relying on a factor calculator, it’s valuable to understand the manual process of finding factors. This knowledge deepens your understanding of number relationships and builds a strong foundation for more advanced mathematical concepts.
Step-by-Step Method for Finding Factors

- Start with the number 1, which is a factor of every integer
- Divide the target number by 1 and record both 1 and the result as factors
- Try dividing by 2, and if there’s no remainder, record both 2 and the result as factors
- Continue this process with consecutive integers up to the square root of the target number
- Arrange all the identified factors in ascending order
Example: Finding Factors of 24
| Division Operation | Result | Remainder | Is it a factor? |
| 24 ÷ 1 | 24 | 0 | Yes, 1 and 24 are factors |
| 24 ÷ 2 | 12 | 0 | Yes, 2 and 12 are factors |
| 24 ÷ 3 | 8 | 0 | Yes, 3 and 8 are factors |
| 24 ÷ 4 | 6 | 0 | Yes, 4 and 6 are factors |
| 24 ÷ 5 | 4.8 | 4 | No |
Therefore, the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24.
While finding factors manually is educational, a factor calculator can instantly provide all factors for any number, making it an invaluable tool for complex calculations or when working with large numbers.
Understanding Factor Pairs
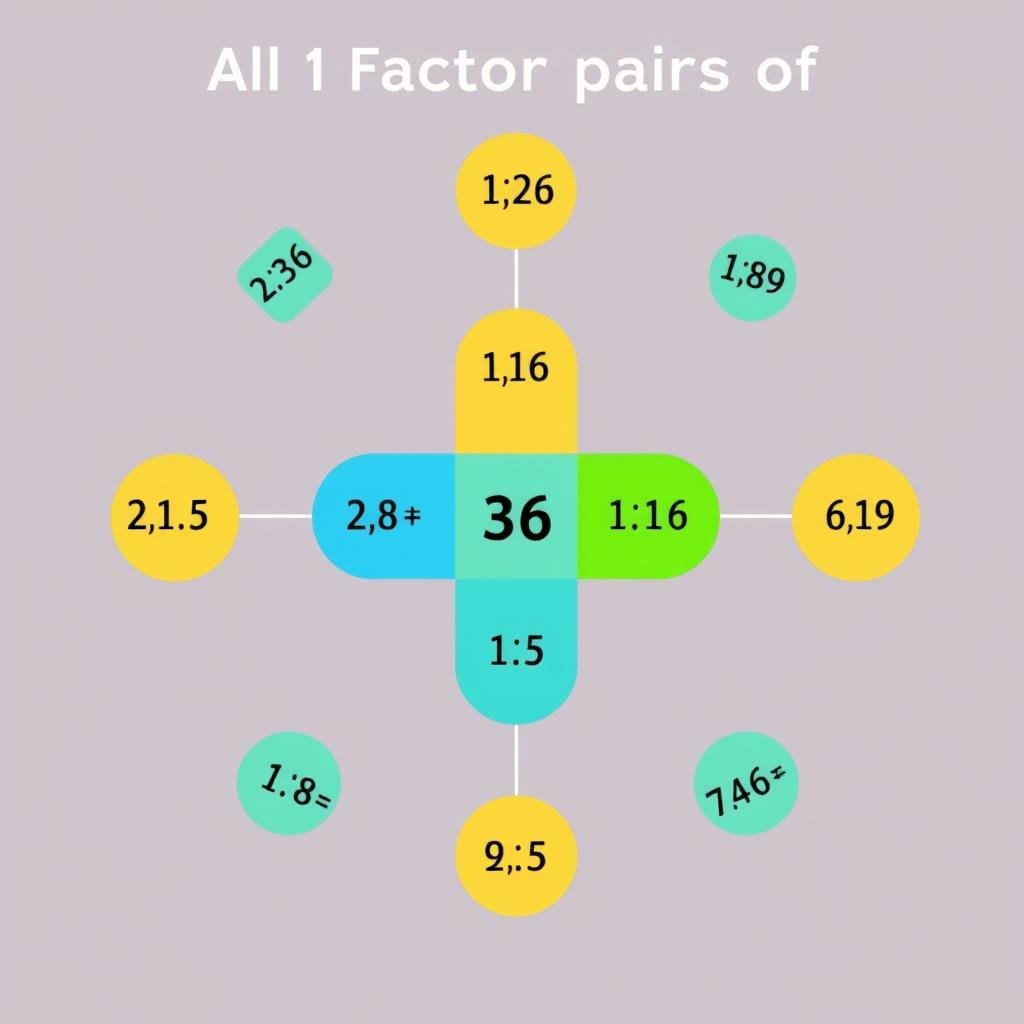
Factor pairs are two numbers that, when multiplied together, equal the target number. For every factor, there is a corresponding factor that forms a pair. For example, the factor pairs of 24 are:
- 1 × 24 = 24
- 2 × 12 = 24
- 3 × 8 = 24
- 4 × 6 = 24
Understanding factor pairs is particularly useful in:
- Geometric representations of numbers
- Problem-solving in algebra
- Factoring quadratic expressions
- Finding the dimensions of rectangles with a given area
A factor calculator can quickly identify all factor pairs for any number, making it easier to visualize and work with these mathematical relationships.
Prime Factorization and Factor Trees

Factor tree showing the prime factorization of 60
Prime factorization is the process of expressing a number as a product of its prime factors. Prime factors are prime numbers that divide the target number evenly. This concept is fundamental in number theory and has applications in cryptography, computer science, and various mathematical fields.
How to Create a Factor Tree
A factor tree is a visual tool that helps find the prime factorization of a number:
- Start with the target number at the top of the tree
- Find any two factors of this number and create branches to them
- If a factor is prime, circle it and stop that branch
- If a factor is not prime, continue branching until all branches end with prime numbers
- The prime factorization is the product of all circled prime numbers
Factor trees for different numbers
Example: Prime Factorization of 36
Let’s find the prime factorization of 36 using a factor tree:
- 36 can be split into 4 × 9
- 4 can be split into 2 × 2
- 9 can be split into 3 × 3
- 2, 3 are prime numbers, so we circle them
- The prime factorization of 36 is 2² × 3²
Need Help with Prime Factorization?
Our Factor Calculator can instantly generate prime factorizations and factor trees for any number, making complex calculations simple.
Greatest Common Factor (GCF) and Least Common Multiple (LCM)

Visualizing GCF and LCM for 12 and 18
The Greatest Common Factor (GCF) and Least Common Multiple (LCM) are important concepts related to factors that have numerous applications in mathematics.
Greatest Common Factor (GCF)
The GCF of two or more numbers is the largest positive integer that divides each of them without a remainder. Finding the GCF is essential for:
- Simplifying fractions
- Factoring algebraic expressions
- Solving problems involving common groupings
Methods to Find the GCF:
Listing Factors Method
- List all factors of each number
- Identify the common factors
- Select the largest common factor
Prime Factorization Method
- Find the prime factorization of each number
- Identify the common prime factors
- Multiply the common prime factors

Least Common Multiple (LCM)
The LCM of two or more numbers is the smallest positive number that is divisible by each of them without a remainder. The LCM is used for:
- Finding common denominators
- Solving problems involving cycles or patterns
- Working with fractions and ratios
A factor calculator can quickly determine both the GCF and LCM of multiple numbers, making these calculations efficient and error-free.
Practical Applications of Factors
Understanding factors and having access to a factor calculator has numerous practical applications beyond academic mathematics:
Education
- Simplifying fractions in arithmetic
- Factoring polynomials in algebra
- Understanding number theory concepts
- Solving mathematical puzzles and problems
Science & Engineering
- Calculating gear ratios in mechanics
- Optimizing dimensions in design
- Analyzing frequency patterns in physics
- Solving problems in computer algorithms
Everyday Life
- Planning schedules and time management
- Dividing resources equally among groups
- Understanding musical rhythm and time signatures
- Solving puzzles and brain teasers
Cryptography and Security
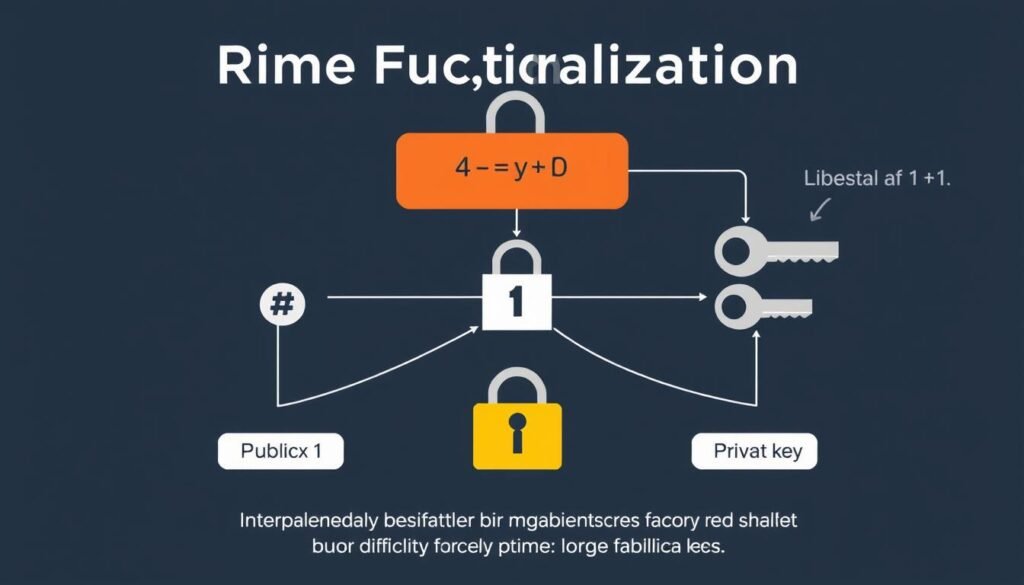
One of the most significant applications of factoring, particularly prime factorization, is in cryptography. Modern encryption methods like RSA rely on the fact that factoring very large numbers into their prime components is extremely difficult and time-consuming. This mathematical challenge forms the foundation of secure internet communications, online banking, and digital signatures.
Apply Factoring to Real-World Problems
Our Factor Calculator helps you apply factoring concepts to practical problems in education, science, engineering, and everyday life.
Key Features of Our Factor Calculator
Our factor calculator offers a comprehensive suite of tools to handle various factoring operations efficiently:
Basic Features
- Find all factors of any positive integer
- Identify factor pairs
- Determine if a number is prime
- Calculate the number of factors
- Generate visual factor trees
Advanced Features
- Prime factorization with exponents
- Calculate GCF of multiple numbers
- Find LCM of multiple numbers
- Factor polynomials and algebraic expressions
- Step-by-step solutions with explanations

Benefits of Using Our Factor Calculator
- Instant results for any number, regardless of size
- Eliminates calculation errors
- Provides step-by-step explanations for educational purposes
- Handles multiple factoring operations simultaneously
- Accessible on any device with internet access
Advantages
- Time-consuming for large numbers
- Prone to human error
- Difficult to verify without recalculation
- Challenging for complex factorization problems
- Requires strong mathematical background
Limitations of Manual Factoring
Conclusion: Mastering Factors with Our Calculator
Factors are fundamental building blocks in mathematics that help us understand number relationships and solve a wide range of problems. While learning to find factors manually is important for building mathematical intuition, a factor calculator provides an efficient and accurate tool for handling complex calculations.
Our factor calculator offers comprehensive features for finding factors, factor pairs, prime factorization, greatest common factors, and least common multiples. Whether you’re a student, teacher, professional, or math enthusiast, this tool can enhance your mathematical capabilities and save valuable time.

By combining mathematical understanding with the power of our factor calculator, you can tackle factoring challenges with confidence and apply these concepts to real-world problems in education, science, engineering, and everyday life.
Ready to Simplify Your Math Calculations?
Our Factor Calculator is free to use and provides instant, accurate results for all your factoring needs.