Fractions are fundamental mathematical concepts that represent parts of a whole. Whether you’re a student tackling math homework, a teacher preparing lesson plans, or a professional working with measurements, understanding how to calculate fractions is an essential skill. Our comprehensive guide explains everything you need to know about fraction operations, from basic addition to complex division, with step-by-step examples to enhance your mathematical proficiency.
Understanding Fractions: The Building Blocks
A fraction consists of two essential parts: the numerator (top number) and the denominator (bottom number). The numerator represents the number of parts we’re working with, while the denominator indicates the total number of equal parts that make up a whole. For example, in the fraction 3/4, the numerator 3 shows we have three parts, and the denominator 4 tells us that the whole is divided into four equal parts.
Types of Fractions
- Proper Fractions: When the numerator is less than the denominator (e.g., 2/5)
- Improper Fractions: When the numerator is greater than or equal to the denominator (e.g., 7/4)
- Mixed Numbers: A whole number and a proper fraction combined (e.g., 1 3/4)
- Equivalent Fractions: Fractions that represent the same value (e.g., 1/2 and 2/4)
Ready to Work with Fractions?
Our Fraction Calculator handles all types of fractions and shows you the step-by-step solution.
Adding Fractions: Step-by-Step Guide
Adding fractions requires finding a common denominator when the denominators differ. This process ensures we’re combining like parts of a whole. Let’s explore how to add fractions effectively.
Adding Fractions with the Same Denominator
When fractions share the same denominator, simply add the numerators while keeping the denominator the same.
Example: 2/5 + 1/5 = (2+1)/5 = 3/5
Adding Fractions with Different Denominators
To add fractions with different denominators, we must first find the least common denominator (LCD) – the smallest number that both denominators can divide into evenly.
- Find the least common denominator (LCD) of the fractions
- Convert each fraction to an equivalent fraction with the LCD
- Add the numerators while keeping the common denominator
- Simplify the result to its lowest terms if possible
Example: 1/4 + 2/3
LCD of 4 and 3 is 12
1/4 = 3/12 and 2/3 = 8/12
3/12 + 8/12 = 11/12

Adding Complex Fractions?
Let our Fraction Calculator do the work for you. Get instant results with detailed steps.
Subtracting Fractions: Complete Method
Subtracting fractions follows a similar process to addition. The key is ensuring both fractions have the same denominator before performing the operation.
Subtracting Fractions with the Same Denominator
When the denominators are the same, simply subtract the numerators while keeping the denominator unchanged.
Example: 5/8 – 3/8 = (5-3)/8 = 2/8 = 1/4

Subtracting Fractions with Different Denominators
For fractions with different denominators, find the least common denominator first, then convert both fractions before subtracting.
Example: 5/6 – 1/3
LCD of 6 and 3 is 6
5/6 remains 5/6 and 1/3 = 2/6
5/6 – 2/6 = 3/6 = 1/2

Need to Subtract Fractions?
Our Fraction Calculator handles subtraction with ease, showing you every step of the process.
Multiplying Fractions: Simplified Approach
Multiplying fractions is straightforward compared to addition and subtraction, as it doesn’t require finding a common denominator. Simply multiply the numerators together and the denominators together.
Basic Multiplication Steps
- Multiply the numerators together
- Multiply the denominators together
- Simplify the resulting fraction if possible
Example: 2/3 × 3/4
Numerators: 2 × 3 = 6
Denominators: 3 × 4 = 12
Result: 6/12 = 1/2
Multiplying Mixed Numbers
When multiplying mixed numbers, first convert them to improper fractions, then multiply as usual.
Example: 1 1/2 × 2 1/3
Convert to improper fractions: 3/2 × 7/3
Multiply: 3/2 × 7/3 = 21/6 = 7/2 = 3 1/2
Multiplying Complex Fractions?
Our Fraction Calculator handles mixed numbers and improper fractions with ease.
Dividing Fractions: The Keep-Change-Flip Method
Division of fractions uses a special technique often remembered as “keep-change-flip.” This means keeping the first fraction, changing the division sign to multiplication, and flipping (finding the reciprocal of) the second fraction.
Division Steps
- Keep the first fraction as is
- Change the division sign to multiplication
- Flip the second fraction (reciprocal)
- Multiply the fractions
- Simplify if possible
Example: 2/3 ÷ 1/4
Keep: 2/3
Change: × (instead of ÷)
Flip: 4/1
Calculate: 2/3 × 4/1 = 8/3 = 2 2/3

Dividing Fractions Made Easy
Our Fraction Calculator handles division with the keep-change-flip method automatically.
Simplifying Fractions and Finding Equivalent Forms
Simplifying fractions means reducing them to their lowest terms, making them easier to work with and understand. This process involves finding the greatest common factor (GCF) of the numerator and denominator.
Steps to Simplify Fractions
- Find the greatest common factor (GCF) of the numerator and denominator
- Divide both the numerator and denominator by the GCF
- The resulting fraction is in its simplest form
Example: Simplify 12/18
GCF of 12 and 18 is 6
12 ÷ 6 = 2
18 ÷ 6 = 3
Simplified fraction: 2/3
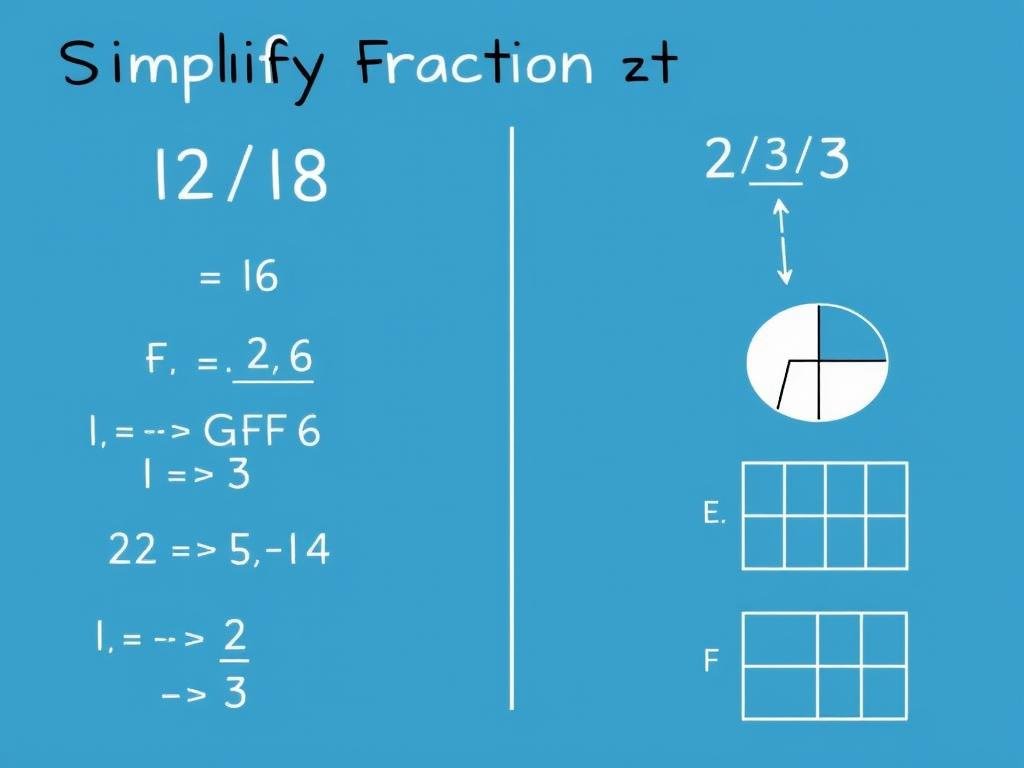
Converting Between Improper Fractions and Mixed Numbers
Converting between improper fractions and mixed numbers is a common operation when working with fractions larger than one whole.
Improper Fraction to Mixed Number
- Divide the numerator by the denominator
- The quotient becomes the whole number
- The remainder becomes the new numerator
- The denominator stays the same
Mixed Number to Improper Fraction
- Multiply the whole number by the denominator
- Add the result to the numerator
- This sum becomes the new numerator
- The denominator stays the same
Example 1: Convert 17/4 to a mixed number
17 ÷ 4 = 4 with remainder 1
Mixed number: 4 1/4
Example 2: Convert 2 3/5 to an improper fraction
(2 × 5) + 3 = 13
Improper fraction: 13/5

Real-World Applications of Fraction Calculations
Fractions are not just abstract mathematical concepts—they have numerous practical applications in everyday life and various professions. Understanding how to work with fractions can help you solve real-world problems efficiently.
Cooking and Baking

Recipes often use fractions for ingredient measurements. You might need to halve or double a recipe, requiring fraction multiplication or division.
Construction and Carpentry

Measurements in construction frequently use fractions of inches. Carpenters must add, subtract, and convert these measurements precisely.
Finance and Budgeting
Budgeting often involves allocating fractions of income to different expenses. Investment returns and interest rates also use fractional calculations.
Solve Real-World Fraction Problems
Whether for recipes, DIY projects, or financial planning, our Fraction Calculator helps you get precise results.
Tips and Tricks for Working with Fractions
Mastering fractions becomes easier with these practical strategies and shortcuts that can help you work more efficiently with fraction calculations.
Mental Math Shortcuts
- Benchmark Fractions: Memorize common fraction equivalents (1/4 = 0.25, 1/3 ≈ 0.33, 1/2 = 0.5)
- Cross-Multiplication: To compare fractions like 3/4 and 5/7, cross-multiply (3×7 vs. 4×5) to see which is larger
- Halving and Doubling: When dividing by 1/2, you can simply multiply by 2 instead
Common Mistakes to Avoid
- Adding Denominators: Remember that 1/2 + 1/3 is NOT 2/5
- Canceling Incorrectly: In 16/64, you can’t just cancel the 6’s
- Forgetting to Simplify: Always check if your answer can be reduced to lowest terms
- Mixing Operations: Division of fractions requires the reciprocal, while addition requires common denominators

How do I know when to use the least common denominator?
You need to find the least common denominator (LCD) when adding or subtracting fractions with different denominators. The LCD is the smallest number that is divisible by all the denominators in your problem. For multiplication and division, you don’t need to find a common denominator.
Why do we invert the second fraction when dividing?
Division by a fraction is equivalent to multiplication by its reciprocal. This is because dividing by a fraction like 1/4 means asking “how many 1/4 pieces are in our number?” Since 1/4 is a smaller unit than 1, the answer will be larger than the original number. Multiplying by 4/1 gives us this correct larger result.
Mastering Fraction Calculations
Understanding how to work with fractions is a fundamental mathematical skill that has countless applications in everyday life. From cooking and construction to finance and education, the ability to add, subtract, multiply, and divide fractions accurately opens doors to better problem-solving and decision-making.
While manual fraction calculations can be challenging, the step-by-step methods outlined in this guide provide a solid foundation for mastering these essential operations. Remember that practice is key to becoming proficient with fractions, and using tools like our Fraction Calculator can help verify your work and deepen your understanding of the underlying concepts.
Ready to Master Fraction Calculations?
Our Fraction Calculator handles all operations with step-by-step solutions to help you learn.