Half-life is a fundamental concept in physics, chemistry, and pharmacology that describes the time required for a substance to decrease to half of its initial value. Whether you’re studying radioactive isotopes, drug metabolism, or carbon dating, understanding how to calculate half-life is essential. This comprehensive guide explains the principles behind half-life calculations, provides step-by-step instructions for solving problems, and explores real-world applications across multiple scientific disciplines.
What is Half-Life?
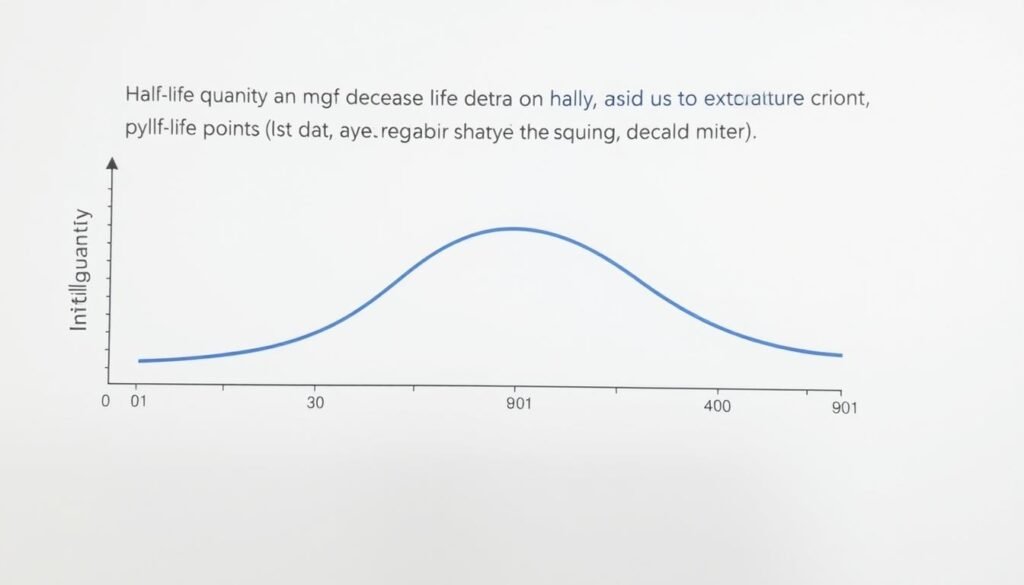
Exponential decay curve showing how quantity decreases by half at regular intervals
Half-life refers to the time it takes for a quantity to reduce to half of its original amount. This concept applies to many natural processes that follow exponential decay patterns. In radioactive decay, half-life is the time required for half of the unstable nuclei in a sample to undergo decay. In pharmacology, it represents the time needed for the concentration of a drug in the bloodstream to decrease by 50%.
The half-life of a substance remains constant regardless of how much of the substance is present. This means that after one half-life period, 50% of the original amount remains. After two half-life periods, 25% remains. After three half-life periods, 12.5% remains, and so on.
Half-lives can range from fractions of a second (for highly unstable isotopes) to billions of years (for slowly decaying elements like uranium-238). This wide range makes half-life calculations essential across numerous scientific fields.
The Half-Life Formula

The fundamental half-life formula showing relationship between initial and remaining quantities
The basic half-life formula is expressed as:
N(t) = N₀ × (1/2)^(t/T)
Where:
- N(t) = Quantity remaining after time t
- N₀ = Initial quantity
- t = Elapsed time
- T = Half-life
This equation can be rearranged to solve for different variables depending on what information you have available. For example, to calculate the half-life when you know the initial quantity, remaining quantity, and elapsed time:
T = t × log(2) / log(N₀/N(t))
To find the time elapsed when you know the half-life, initial quantity, and remaining quantity:
t = T × log(N₀/N(t)) / log(2)
These formulas form the foundation of half-life calculations across all applications, from radioactive decay to drug metabolism.
Decay Constant and Mean Lifetime
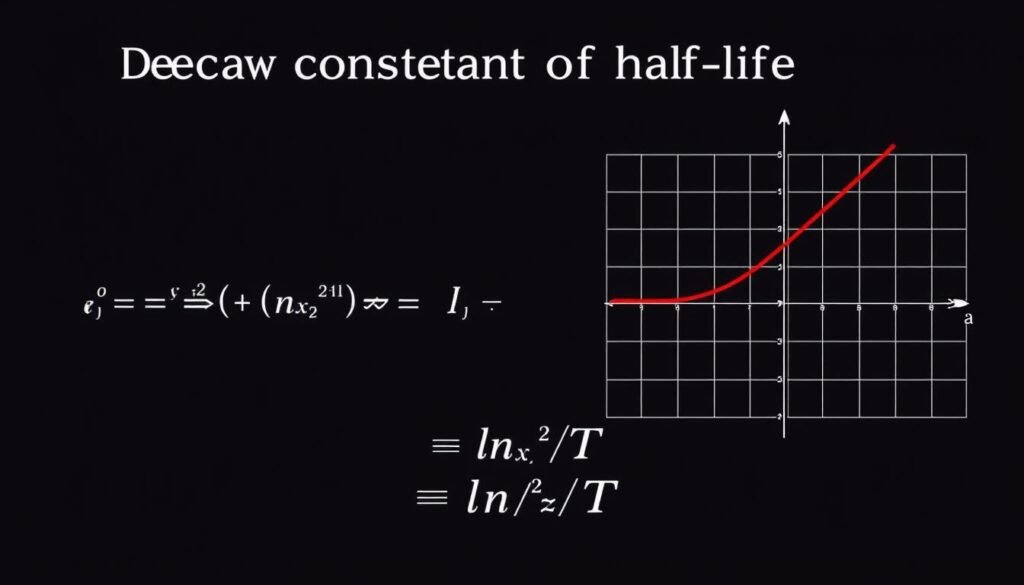
Relationship between decay constant (λ) and half-life (T)
The decay constant (λ) is another important parameter in half-life calculations. It represents the probability per unit time that a given nucleus or molecule will decay. The decay constant is related to half-life by the equation:
λ = ln(2) / T ≈ 0.693 / T
Where:
- λ = Decay constant
- T = Half-life
- ln(2) = Natural logarithm of 2 (approximately 0.693)
The mean lifetime (τ) is the average time that all atoms in a sample exist before decaying. It’s related to the decay constant by:
τ = 1 / λ
And to half-life by:
τ = T / ln(2) ≈ T / 0.693
Understanding these relationships allows scientists to express decay rates in different but equivalent ways depending on the specific application.
How to Calculate Half-Life
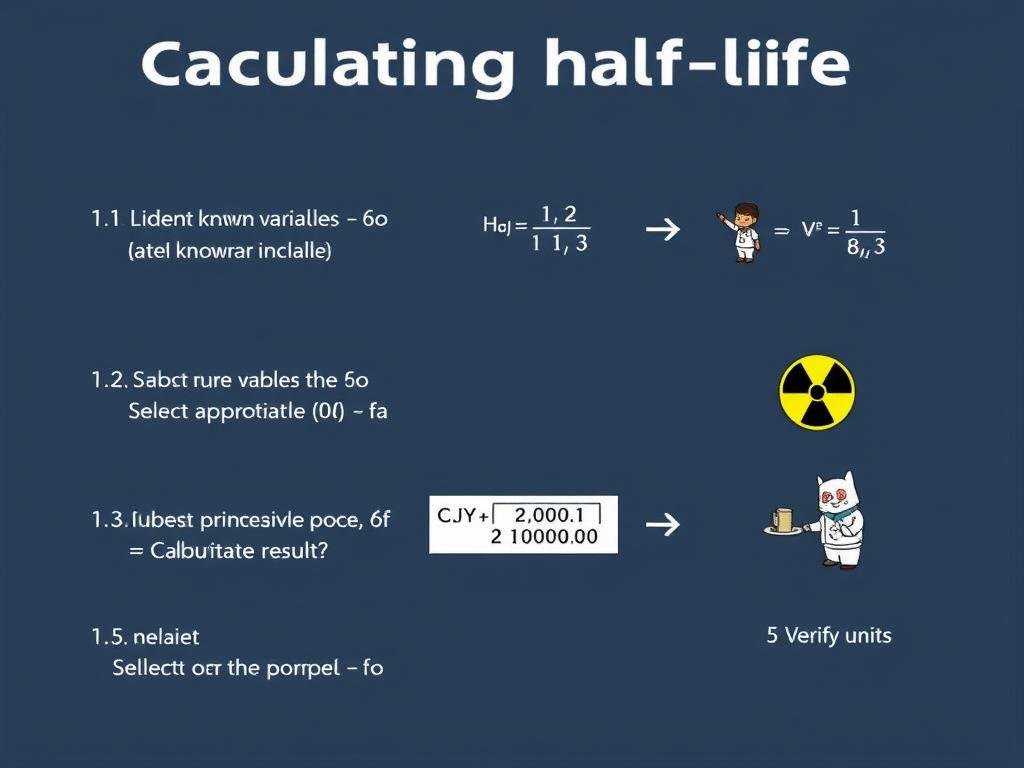
Step-by-step process for calculating half-life
Step-by-Step Method
- Identify what you know: Determine which variables you already have (initial quantity, current quantity, elapsed time, or half-life).
- Select the appropriate formula: Choose the equation that allows you to solve for your unknown variable.
- Substitute the values: Insert your known values into the formula.
- Solve the equation: Calculate the result using logarithms when necessary.
- Verify units: Ensure your answer has the correct units (time units for half-life, quantity units for amounts).
Example Calculation
A radioactive sample initially contains 800 mg of material. After 20 minutes, only 50 mg remains. What is the half-life of this radioactive substance?
Solution:
- We know: N₀ = 800 mg, N(t) = 50 mg, t = 20 minutes
- We need to find T (half-life)
- Using the formula: T = t × log(2) / log(N₀/N(t))
- T = 20 × log(2) / log(800/50)
- T = 20 × 0.301 / 1.204
- T = 5 minutes
Therefore, the half-life of this radioactive substance is 5 minutes.
Common Applications of Half-Life Calculations

Radioactive decay measurements
Nuclear Physics
In nuclear physics, half-life calculations are essential for understanding radioactive decay processes, nuclear waste management, and nuclear power generation. Scientists use half-life data to determine the age of rocks and artifacts through radiometric dating techniques.
Drug metabolism in pharmacology
Pharmacology
In pharmacology, half-life determines how long a drug remains active in the body. This information helps doctors establish dosing schedules and understand drug accumulation. For example, a drug with a short half-life might require multiple daily doses, while one with a long half-life might be taken once daily.

Carbon dating in archaeology
Archaeology
Carbon dating relies on the half-life of carbon-14 (5,730 years) to determine the age of organic materials up to about 50,000 years old. By measuring the ratio of carbon-14 to stable carbon-12, archaeologists can calculate when an organism died and stopped incorporating new carbon.
Half-Life Examples in Different Fields
| Element/Substance | Half-Life | Application |
| Carbon-14 | 5,730 years | Archaeological dating |
| Uranium-238 | 4.5 billion years | Geological dating |
| Iodine-131 | 8.02 days | Medical treatments |
| Acetaminophen | 1-4 hours | Pain relief dosing |
| Amiodarone | 26-107 days | Cardiac arrhythmia treatment |
| Epinephrine | 2-3 minutes | Emergency medicine |

Comparison of half-lives across different substances on a logarithmic scale
Understanding Exponential Decay
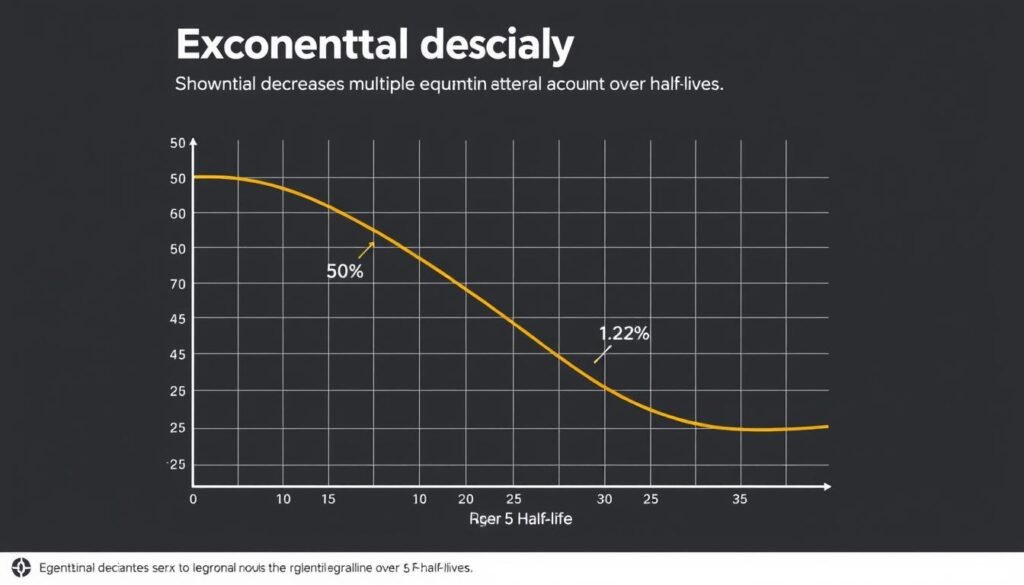
Exponential decay over multiple half-life periods
Half-life is a manifestation of exponential decay, a fundamental pattern in nature where the rate of decrease is proportional to the current value. This creates a distinctive curve where the quantity never quite reaches zero but becomes increasingly smaller with each half-life period.
Key Properties of Exponential Decay
- Constant proportion: The same fraction of substance decays in each equal time period
- Never reaches zero: Mathematically, the quantity approaches but never reaches zero
- Predictable pattern: After n half-lives, the remaining fraction is (1/2)ⁿ
- Independent of initial quantity: The decay rate depends only on the current amount, not the starting amount
Remaining Quantity After Multiple Half-Lives
- After 1 half-life: 50% remains
- After 2 half-lives: 25% remains
- After 3 half-lives: 12.5% remains
- After 4 half-lives: 6.25% remains
- After 5 half-lives: 3.125% remains
- After 10 half-lives: 0.0977% remains (less than 0.1%)
Practical Tips for Half-Life Calculations

Laboratory analysis of half-life requires precise measurements and calculations
How do I handle very short or very long half-lives?
For extremely short half-lives (seconds or less), high-precision timing equipment is necessary. For very long half-lives (thousands or millions of years), scientists often use indirect methods or measure the decay products rather than waiting for significant decay to occur.
What if I don’t know the initial quantity?
If you don’t know the initial quantity but have measurements at two different times, you can use the ratio between these measurements to calculate the half-life without needing to know the absolute initial quantity.
How do I account for background radiation in measurements?
Always measure background radiation separately and subtract it from your sample measurements. This ensures that your calculations reflect only the decay of your sample, not environmental radiation.
Can half-life change under different conditions?
For radioactive decay, half-life is generally constant regardless of temperature, pressure, or chemical state. However, for some processes like drug metabolism, the effective half-life can be affected by factors such as liver function, kidney health, and other physiological conditions.
Conclusion
Understanding half-life calculations is essential across numerous scientific disciplines, from nuclear physics to medicine. The concept provides a quantitative way to describe how quickly substances decay or diminish over time. By mastering the formulas and principles outlined in this guide, you can accurately predict the behavior of radioactive materials, medications, and other substances that follow exponential decay patterns.
Whether you’re a student learning the basics of decay processes, a researcher analyzing radioactive samples, or a healthcare professional calculating drug dosages, the ability to calculate half-life is a valuable skill that enhances your scientific understanding and practical capabilities.
Ready to Calculate Half-Life Instantly?
Save time and avoid calculation errors with our easy-to-use Half-Life Calculator. Perfect for students, researchers, and professionals working with radioactive decay, drug metabolism, or carbon dating.