Logarithms are powerful mathematical tools that help solve complex problems in science, engineering, finance, and many other fields. While a log calculator makes these calculations instant, understanding the underlying concepts of logarithmic functions is essential for anyone working with exponential relationships. This comprehensive guide will walk you through everything you need to know about logarithms, from basic definitions to practical applications and manual calculation methods.
What Are Logarithms and How Do They Work?
The fundamental relationship between logarithms and exponents
A logarithm is the inverse operation to exponentiation. When we write logb(x) = y, we’re asking: “To what power (y) must we raise the base (b) to get the number (x)?” In other words, if by = x, then logb(x) = y.
This inverse relationship makes logarithms incredibly useful for solving equations where variables appear in exponents. They allow us to “bring down” exponents and make them easier to work with, which is why they’re essential in fields ranging from compound interest calculations to earthquake measurement.
Master Logarithmic Concepts
Understanding logarithms opens doors to advanced mathematics and real-world applications. Explore our comprehensive resources to build your mathematical foundation.
Types of Logarithms: Common, Natural, and Binary
Common Logarithm (Base 10)
Written as log10(x) or simply log(x), the common logarithm uses base 10 and is frequently used in scientific notation and many engineering applications.
Example: log(100) = 2 because 102 = 100
Natural Logarithm (Base e)
Written as loge(x) or ln(x), the natural logarithm uses the irrational number e (≈2.71828) as its base and is essential in calculus and growth/decay problems.
Example: ln(e) = 1 because e1 = e
Binary Logarithm (Base 2)
Written as log2(x), the binary logarithm is commonly used in computer science and information theory to measure data and algorithm complexity.
Example: log2(8) = 3 because 23 = 8
Comparison of logarithmic curves with different bases
Essential Logarithm Properties and Formulas
Understanding the properties of logarithms is crucial for solving complex equations and simplifying expressions. These rules allow us to break down complicated logarithmic expressions into simpler components.
| Property | Formula | Example |
| Product Rule | logb(x × y) = logb(x) + logb(y) | log(2 × 5) = log(2) + log(5) |
| Quotient Rule | logb(x ÷ y) = logb(x) – logb(y) | log(8 ÷ 2) = log(8) – log(2) |
| Power Rule | logb(xn) = n × logb(x) | log(53) = 3 × log(5) |
| Change of Base | logb(x) = logc(x) ÷ logc(b) | log2(8) = log(8) ÷ log(2) |
| Logarithm of 1 | logb(1) = 0 | log(1) = 0 |
| Logarithm of Base | logb(b) = 1 | log10(10) = 1 |

Visual guide to logarithm properties
Apply Logarithm Properties
Mastering logarithm properties helps solve complex equations with ease. Explore our practice problems to strengthen your skills.
How to Calculate Logarithms Manually: Step-by-Step Guide
While digital tools make logarithm calculations instant, knowing how to calculate them manually deepens your understanding and helps in situations where technology isn’t available.
Method 1: Using the Change of Base Formula
Manual calculation using the change of base formula
- Identify the base (b) and the argument (x) in your logarithm logb(x).
- Apply the change of base formula: logb(x) = log10(x) ÷ log10(b).
- Calculate log10(x) and log10(b) using a scientific calculator or log tables.
- Divide log10(x) by log10(b) to find your answer.
Example: Calculate log3(27)
Step 1: We have b = 3 and x = 27.
Step 2: Apply the formula log3(27) = log10(27) ÷ log10(3).
Step 3: Calculate log10(27) ≈ 1.431 and log10(3) ≈ 0.477.
Step 4: Divide 1.431 ÷ 0.477 ≈ 3.
Therefore, log3(27) = 3, which makes sense since 33 = 27.
Method 2: Using Logarithm Properties
Breaking down complex logarithms using properties
- Break down the argument into simpler components using prime factorization.
- Apply the product, quotient, and power rules to simplify the expression.
- Calculate the logarithms of the simpler components.
- Combine the results according to the logarithm properties.
Example: Calculate log10(24) without a calculator
Step 1: Break down 24 into 8 × 3 or 23 × 3.
Step 2: Apply the product rule: log(24) = log(8 × 3) = log(8) + log(3).
Step 3: Apply the power rule: log(8) = log(23) = 3 × log(2).
Step 4: Using known values: log(2) ≈ 0.301 and log(3) ≈ 0.477.
Step 5: Calculate 3 × 0.301 + 0.477 ≈ 0.903 + 0.477 ≈ 1.38.
Therefore, log10(24) ≈ 1.38.
Real-World Applications of Logarithms

Logarithms in everyday applications
Science and Engineering
- pH Scale: Measures acidity using logarithms of hydrogen ion concentration.
- Richter Scale: Measures earthquake intensity on a logarithmic scale.
- Decibel Scale: Measures sound intensity logarithmically.
- Stellar Brightness: Star magnitude uses a logarithmic scale.
- Radioactive Decay: Modeled using logarithmic functions.
Finance and Economics
- Compound Interest: Calculated using logarithms to find time periods.
- Economic Growth: GDP growth rates use logarithmic models.
- Investment Returns: Log returns are used in financial analysis.
- Rule of 72: Approximates investment doubling time using logarithms.
- Elasticity: Price elasticity of demand uses logarithmic relationships.
Computer Science
- Algorithm Complexity: Big O notation often involves logarithms.
- Binary Search: Has logarithmic time complexity.
- Information Theory: Entropy is measured using logarithms.
- Data Compression: Many algorithms use logarithmic principles.
- Machine Learning: Log-likelihood functions in statistical models.
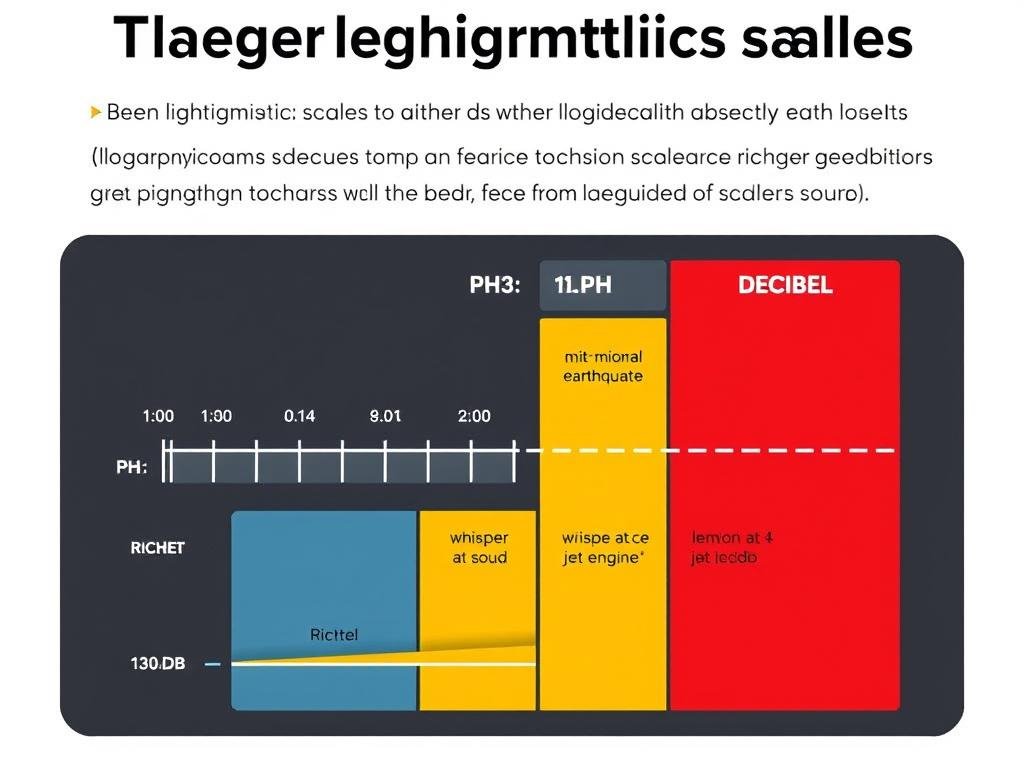
Comparison of logarithmic scales in science
Spotlight: Compound Interest and the Power of Logarithms
One of the most practical applications of logarithms is in financial calculations, particularly for compound interest. If you want to know how long it will take for an investment to double, you can use the logarithmic formula:
Time to double = log(2) ÷ log(1 + r)
Where r is the interest rate in decimal form (e.g., 0.05 for 5%).
This formula is the mathematical basis for the “Rule of 72,” which states that dividing 72 by the interest rate percentage gives an approximation of the years needed to double your investment.
Explore Financial Applications
Discover how logarithms can help you make smarter financial decisions and understand investment growth.
Solving Logarithmic Equations: Techniques and Examples
Logarithmic equations are equations that contain logarithms of variables. Solving them requires understanding logarithm properties and sometimes converting between logarithmic and exponential forms.

Solving logarithmic equations step-by-step
Basic Techniques for Solving Logarithmic Equations
- Convert to exponential form: If logb(x) = y, then x = by.
- Use logarithm properties: Apply product, quotient, and power rules to simplify.
- Combine like terms: Group logarithms with the same base and argument.
- Check solutions: Verify that solutions work in the original equation and respect domain restrictions (arguments must be positive).
Example 1: Simple Logarithmic Equation
Solve log3(x) = 2
Solution:
Convert to exponential form:
log3(x) = 2
x = 32
x = 9
Therefore, x = 9 is the solution.
Example 2: Using Logarithm Properties
Solve log(x) + log(x+3) = log(4x)
Solution:
Using the product rule:
log(x(x+3)) = log(4x)
x(x+3) = 4x
x2 + 3x = 4x
x2 – x = 0
x(x-1) = 0
x = 0 or x = 1
Since x = 0 makes log(x) undefined, the only valid solution is x = 1.

Common mistakes to avoid when solving logarithmic equations
Understanding Logarithmic Functions and Their Graphs
A logarithmic function takes the form f(x) = logb(x), where b is the base. These functions have distinctive properties that make them useful for modeling various phenomena.

Key features of logarithmic functions
Properties of Logarithmic Functions
| Property | Description |
| Domain | All positive real numbers (x > 0) |
| Range | All real numbers |
| Vertical Asymptote | x = 0 (the y-axis) |
| Intercept | The point (1, 0) for any base |
| Growth Rate | Increases very slowly (sub-linear growth) |
| Inverse Function | f-1(x) = bx (exponential function) |
Inverse relationship between logarithmic and exponential functions
Transformations of Logarithmic Functions
Like other functions, logarithmic functions can be transformed through shifts, stretches, and reflections:
- Vertical shift: f(x) = logb(x) + k shifts the graph up (k > 0) or down (k
- Horizontal shift: f(x) = logb(x – h) shifts the graph right (h > 0) or left (h
- Vertical stretch/compression: f(x) = a · logb(x) stretches (|a| > 1) or compresses (0
- Reflection: f(x) = -logb(x) reflects the graph across the x-axis.
Master Function Transformations
Understanding how to transform logarithmic functions helps in modeling real-world phenomena. Explore our interactive examples to see transformations in action.
Frequently Asked Questions About Logarithms
What is the difference between log and ln?
Log (without a specified base) typically refers to the common logarithm with base 10, written as log10. Ln refers specifically to the natural logarithm with base e (approximately 2.71828), written as loge or ln. While both are logarithms, they use different bases for different applications.
Can logarithms be negative?
Yes, logarithms can be negative. If 0 b(x) will be negative for any base b > 1. For example, log10(0.1) = -1 because 10-1 = 0.1.
Why can’t you take the logarithm of a negative number?
Logarithms of negative numbers are undefined in the real number system because there is no real number power that, when applied to a positive base, will result in a negative number. For example, there is no real value of y such that 10y = -5.
What is the value of log(0)?
Log(0) is undefined. As x approaches 0 from the positive side, log(x) approaches negative infinity, but it never actually reaches a finite value at x = 0.
How do I convert between different logarithm bases?
To convert a logarithm from one base to another, use the change of base formula: logb(x) = logc(x) ÷ logc(b), where c is any positive number not equal to 1. For example, to convert log2(8) to base 10, you would calculate log10(8) ÷ log10(2).
What is the logarithm of 1?
The logarithm of 1 is always 0, regardless of the base. This is because any number raised to the power of 0 equals 1. So logb(1) = 0 for any base b.
Visual guide to common logarithm questions
Mastering Logarithms: Key Takeaways
Logarithms are powerful mathematical tools that help us understand exponential relationships and solve complex problems across various fields. From calculating compound interest to measuring earthquake intensity, logarithmic functions provide elegant solutions to real-world challenges.
Benefits of Understanding Logarithms
- Solve exponential equations with ease
- Understand growth and decay models
- Interpret data on logarithmic scales
- Apply mathematical concepts to real-world problems
- Develop stronger analytical thinking skills
Challenges in Learning Logarithms
- Abstract concept that requires practice
- Multiple rules and properties to memorize
- Domain restrictions can cause errors
- Converting between different bases can be confusing
- Applications sometimes require additional context
By understanding the fundamental concepts, properties, and applications of logarithms, you’ve gained valuable mathematical knowledge that extends far beyond simple calculations. Whether you’re a student, professional, or simply curious about mathematics, logarithms provide a fascinating window into the elegant relationships that govern our world.
Continue Your Mathematical Journey
Logarithms are just one fascinating aspect of mathematics. Explore related topics to further expand your knowledge and problem-solving abilities.