Ohm’s Law stands as one of the most fundamental principles in electrical engineering and electronics. This cornerstone equation establishes the relationship between voltage, current, and resistance in electrical circuits. Whether you’re designing a simple LED circuit, troubleshooting complex electronic systems, or studying electrical engineering, understanding Ohm’s Law is essential for success in working with electricity.
In this comprehensive guide, we’ll explore the Ohm’s Law formula, break down its components, demonstrate practical applications, and show you how to perform calculations efficiently. By mastering these concepts, you’ll gain valuable skills for analyzing and designing electrical circuits with confidence.
What is Ohm’s Law?
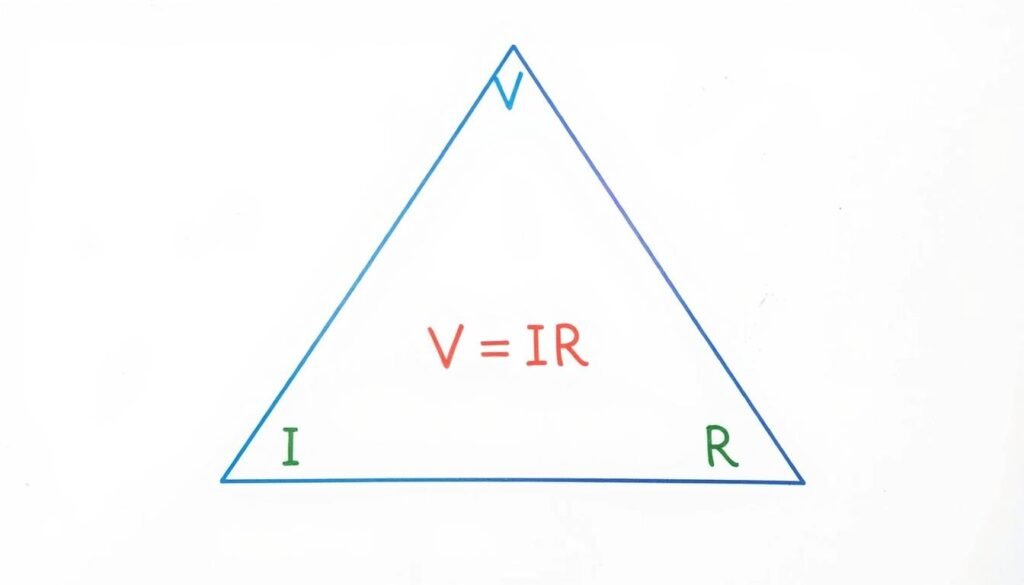
The Ohm’s Law triangle showing the relationship between voltage (V), current (I), and resistance (R)
Ohm’s Law, formulated by German physicist Georg Ohm in 1827, defines the relationship between voltage, current, and resistance in an electrical circuit. In its simplest form, Ohm’s Law states that the current flowing through a conductor between two points is directly proportional to the voltage across those points and inversely proportional to the resistance between them.
This fundamental principle is expressed mathematically as:
V = I × R
Where:
- V represents voltage measured in volts (V)
- I represents current measured in amperes (A)
- R represents resistance measured in ohms (Ω)
The beauty of Ohm’s Law lies in its versatility. By rearranging the formula, you can solve for any of the three variables when the other two are known:
- To find current: I = V ÷ R
- To find resistance: R = V ÷ I
Understanding these relationships is crucial for anyone working with electrical circuits, from students and hobbyists to professional engineers and technicians.
The Ohm’s Law Formula Explained
Ohm’s Law formula wheel showing different variations of the formula including power calculations
Let’s break down each component of Ohm’s Law to gain a deeper understanding of how electrical circuits function:
Voltage (V)
Voltage, measured in volts (V), represents the electrical potential difference between two points in a circuit. Think of voltage as the “electrical pressure” that pushes electrons through a conductor. Common voltage sources include batteries, power supplies, and generators.
In practical terms, a higher voltage means more electrical pressure, which can drive more current through the same resistance. This is why increasing the voltage in a circuit while keeping resistance constant will result in increased current flow.
Current (I)
Current, measured in amperes (A), represents the flow rate of electric charge through a conductor. It indicates how many electrons pass through a point in the circuit per second. Current flows from the positive terminal of a power source through the circuit and back to the negative terminal.
Current is the actual movement of electrical charge, and it’s what performs the useful work in electrical devices. Too much current can damage components or create safety hazards, which is why proper circuit design is essential.
Resistance (R)
Resistance, measured in ohms (Ω), represents the opposition to current flow in an electrical circuit. All materials have some level of resistance, with conductors having low resistance and insulators having high resistance. Resistors are components specifically designed to provide a precise amount of resistance in a circuit.
Resistance converts electrical energy into other forms, typically heat. This property is used in devices like heaters and incandescent light bulbs, but it’s also a factor that engineers must manage to ensure efficient circuit operation.
Simple circuit diagram illustrating Ohm’s Law with a 12V source and 100Ω resistor
Power (P)
While not part of the original Ohm’s Law formula, power calculations are closely related and essential in electrical engineering. Power, measured in watts (W), represents the rate at which electrical energy is transferred or converted in a circuit.
Power can be calculated using several formulas derived from Ohm’s Law:
- P = V × I (Power equals voltage multiplied by current)
- P = I² × R (Power equals current squared multiplied by resistance)
- P = V² ÷ R (Power equals voltage squared divided by resistance)
Understanding power calculations is crucial for selecting appropriate components that can handle the electrical load without overheating or failing.
How to Use the Ohm’s Law Formula
Applying Ohm’s Law to solve electrical problems is straightforward once you understand the basic principles. Let’s walk through examples of how to calculate each variable when the other two are known.

Step-by-step calculation of voltage using Ohm’s Law
Example 1: Finding Voltage
If you know the current and resistance in a circuit, you can calculate the voltage using V = I × R.
Given: Current (I) = 2 amperes, Resistance (R) = 6 ohms
Formula: V = I × R
Calculation: V = 2A × 6Ω = 12 volts
Therefore, the voltage across the resistor is 12 volts.
Example 2: Finding Current
If you know the voltage and resistance, you can calculate the current using I = V ÷ R.
Given: Voltage (V) = 9 volts, Resistance (R) = 3 ohms
Formula: I = V ÷ R
Calculation: I = 9V ÷ 3Ω = 3 amperes
Therefore, the current flowing through the circuit is 3 amperes.

Step-by-step calculation of resistance using Ohm’s Law
Example 3: Finding Resistance
If you know the voltage and current, you can calculate the resistance using R = V ÷ I.
Given: Voltage (V) = 24 volts, Current (I) = 4 amperes
Formula: R = V ÷ I
Calculation: R = 24V ÷ 4A = 6 ohms
Therefore, the resistance in the circuit is 6 ohms.
Example 4: Calculating Power
Let’s calculate the power in a circuit where voltage and current are known.
Given: Voltage (V) = 12 volts, Current (I) = 2 amperes
Formula: P = V × I
Calculation: P = 12V × 2A = 24 watts
Therefore, the power dissipated in the circuit is 24 watts.

Power calculation using Ohm’s Law in a practical circuit
Pro Tip: When working with Ohm’s Law, always pay attention to units. Voltage should be in volts, current in amperes, and resistance in ohms to ensure accurate calculations.
Practical Applications of Ohm’s Law
Ohm’s Law isn’t just a theoretical concept—it has numerous practical applications in everyday electronics and electrical engineering. Understanding these applications helps demonstrate the real-world value of mastering this fundamental principle.

Practical applications of Ohm’s Law in electronic circuit design and troubleshooting
Circuit Design
When designing electrical circuits, engineers use Ohm’s Law to:
- Calculate the appropriate resistor values to limit current to LEDs and other components
- Determine power ratings for resistors to prevent overheating
- Design voltage divider circuits for sensing and measurement applications
- Calculate the values needed for pull-up and pull-down resistors in digital circuits
Troubleshooting
Technicians regularly apply Ohm’s Law when troubleshooting electrical problems:
- Predicting expected voltage drops across components
- Verifying if a resistor has the correct value or has failed
- Determining if current flow is within acceptable limits
- Identifying potential short circuits or open circuits

LED circuit with current limiting resistor designed using Ohm’s Law
Power Distribution
Ohm’s Law is crucial in power distribution systems:
- Calculating voltage drops in power transmission lines
- Sizing conductors appropriately for current-carrying capacity
- Determining power losses in electrical systems
- Designing circuit protection devices like fuses and circuit breakers
Battery-Powered Devices
For portable and battery-powered devices, Ohm’s Law helps:
- Calculate expected battery life based on current draw
- Design efficient power management circuits
- Select appropriate components to maximize battery efficiency
- Determine charging requirements and circuitry
Voltage divider circuit designed using Ohm’s Law for sensor applications
Why Use an Online Ohm’s Law Calculator?
While understanding the manual calculations is essential, using an Ohm’s Law calculator offers several advantages for both beginners and professionals:

Using an Ohm’s Law calculator for quick and accurate electrical calculations
Speed and Efficiency
An Ohm’s Law calculator provides instant results without the need for manual calculations. This is particularly valuable when working with complex circuits or when you need to try different values quickly to find the optimal solution.
Accuracy
Calculators eliminate human error in calculations, ensuring precise results every time. This is crucial in electrical engineering where even small errors can lead to component failure or safety hazards.
Learning Tool
For students and beginners, an Ohm’s Law calculator serves as an excellent learning tool. It allows you to verify your manual calculations and understand the relationships between voltage, current, and resistance through experimentation.
Comprehensive Calculations
Many Ohm’s Law calculators provide additional calculations beyond the basic formula, such as power calculations, which are essential for complete circuit analysis and component selection.
Comparison of manual calculations versus using an Ohm’s Law calculator
Master Electrical Calculations with Ohm’s Law
Understanding Ohm’s Law is fundamental to success in electrical engineering and electronics. By mastering these principles, you’ll be able to design, analyze, and troubleshoot circuits with confidence. Whether you’re a student, hobbyist, or professional, the ability to apply Ohm’s Law correctly will serve you throughout your electrical journey.
Limitations of Ohm’s Law
While Ohm’s Law is incredibly useful, it’s important to understand its limitations:
Materials and components where Ohm’s Law has limitations or does not apply
- Non-linear components: Ohm’s Law applies to linear resistors but not to components like diodes, transistors, and certain specialized resistors whose resistance changes with voltage or current.
- Temperature effects: The law assumes constant temperature, but in reality, resistance often changes with temperature.
- High frequencies: At very high frequencies, additional factors like capacitance and inductance become significant, complicating the simple V=IR relationship.
- Superconductors: These materials have zero resistance under certain conditions, which falls outside the normal application of Ohm’s Law.
Understanding these limitations helps engineers know when to apply Ohm’s Law directly and when more complex analysis is required.
Conclusion
Ohm’s Law remains one of the most fundamental and practical principles in electrical engineering. By understanding the relationship between voltage, current, and resistance, you gain the foundation needed to analyze, design, and troubleshoot electrical circuits effectively.
Whether you’re calculating the appropriate resistor for an LED circuit, determining power requirements for a new design, or troubleshooting an electrical problem, Ohm’s Law provides the essential framework for your analysis. While online calculators offer convenience and accuracy, understanding the underlying principles ensures you can apply this knowledge creatively to solve real-world electrical challenges.
Continue exploring electrical concepts and practicing calculations to build your expertise. The more you work with Ohm’s Law, the more intuitive electrical relationships will become, empowering you to tackle increasingly complex electrical projects with confidence.
What is the difference between AC and DC when applying Ohm’s Law?
Ohm’s Law applies to both AC and DC circuits, but with AC circuits, you need to consider impedance rather than just resistance. Impedance includes the effects of resistance, capacitance, and inductance. For pure DC circuits, Ohm’s Law can be applied directly using resistance only.
Can Ohm’s Law be used for parallel circuits?
Yes, Ohm’s Law applies to both series and parallel circuits. In parallel circuits, the voltage is the same across all components, but the current divides. You can use Ohm’s Law to calculate the current through each parallel path by dividing the voltage by the resistance of that specific path.
How does Ohm’s Law relate to Kirchhoff’s Laws?
Ohm’s Law complements Kirchhoff’s Laws in circuit analysis. While Ohm’s Law describes the relationship between voltage, current, and resistance for individual components, Kirchhoff’s Laws describe how current and voltage behave throughout an entire circuit. Together, they provide a complete framework for analyzing complex circuits.