Calculate probabilities instantly with our easy-to-use Probability Calculator. Perfect for students, professionals, and anyone needing fast, accurate results.
Probability Calculator
Understanding probability is essential in statistics, mathematics, gaming, finance, and everyday decision-making. A probability calculator helps you determine the likelihood of events occurring, from simple coin tosses to complex conditional scenarios. This comprehensive guide explains probability concepts, calculation methods, and how our probability calculator can simplify these often challenging calculations.
What is Probability?

Probability measures the likelihood of events on a scale from 0 (impossible) to 1 (certain)
Probability is the mathematical measure of the likelihood that an event will occur. It’s quantified as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. The higher the probability of an event, the more likely it is to occur.
Probability can be expressed in several ways:
- As a fraction (1/6)
- As a decimal (0.167)
- As a percentage (16.7%)
The basic probability formula is:
P(E) = Number of favorable outcomes / Total number of possible outcomes
Where P(E) represents the probability of event E occurring.
Need Quick Probability Calculations?
Skip the manual calculations and get instant results with our easy-to-use probability calculator.
Types of Probability
Understanding different types of probability is crucial for applying the right calculation methods to your specific scenario.
Single Event Probability

Single event probability measures the likelihood of one specific outcome occurring in a random experiment. For example, the probability of rolling a 6 on a fair die is 1/6 (approximately 0.167 or 16.7%).
Multiple Events Probability
When calculating probabilities involving multiple events, we need to consider whether these events are independent or dependent.
Independent Events
Independent events are those where the occurrence of one event does not affect the probability of another event. For example, when flipping a coin twice, the outcome of the first flip doesn’t influence the second flip.
For independent events A and B:
P(A and B) = P(A) × P(B)
Dependent Events
Dependent events are those where the occurrence of one event affects the probability of another event. For example, when drawing cards from a deck without replacement, the probability of drawing a specific card changes after each draw.
For dependent events A and B:
P(A and B) = P(A) × P(B|A)
Where P(B|A) is the conditional probability of B given that A has occurred.
Conditional Probability
Conditional probability measures the likelihood of an event occurring given that another event has already occurred. It’s denoted as P(A|B), read as “the probability of A given B.”
P(A|B) = P(A and B) / P(B)
Calculate Complex Probabilities Instantly
Our probability calculator handles single events, independent events, and conditional probability with ease.
Essential Probability Formulas

Mastering these fundamental probability formulas will help you solve a wide range of probability problems.
Basic Probability Formula
For a single event E:
P(E) = Number of favorable outcomes / Total number of possible outcomes
Complement Rule
The probability that an event will not occur:
P(not E) = 1 – P(E)
Addition Rule
For the probability of either event A or event B occurring:
P(A or B) = P(A) + P(B) – P(A and B)
For mutually exclusive events: P(A or B) = P(A) + P(B)
Multiplication Rule
For the probability of both events A and B occurring:
For independent events: P(A and B) = P(A) × P(B)
For dependent events: P(A and B) = P(A) × P(B|A)
Bayes’ Theorem
For finding conditional probability when you know the reverse conditional:
P(A|B) = [P(B|A) × P(A)] / P(B)
When to Use Addition Rule
Use the addition rule when calculating the probability of either one event OR another event occurring.
Example: Finding the probability of drawing either a heart OR a face card from a deck.
When to Use Multiplication Rule
Use the multiplication rule when calculating the probability of one event AND another event both occurring.
Example: Finding the probability of drawing two aces in a row from a deck.
Step-by-Step Probability Examples
Let’s work through some practical examples to demonstrate how to calculate different types of probabilities.
Example 1: Single Event Probability
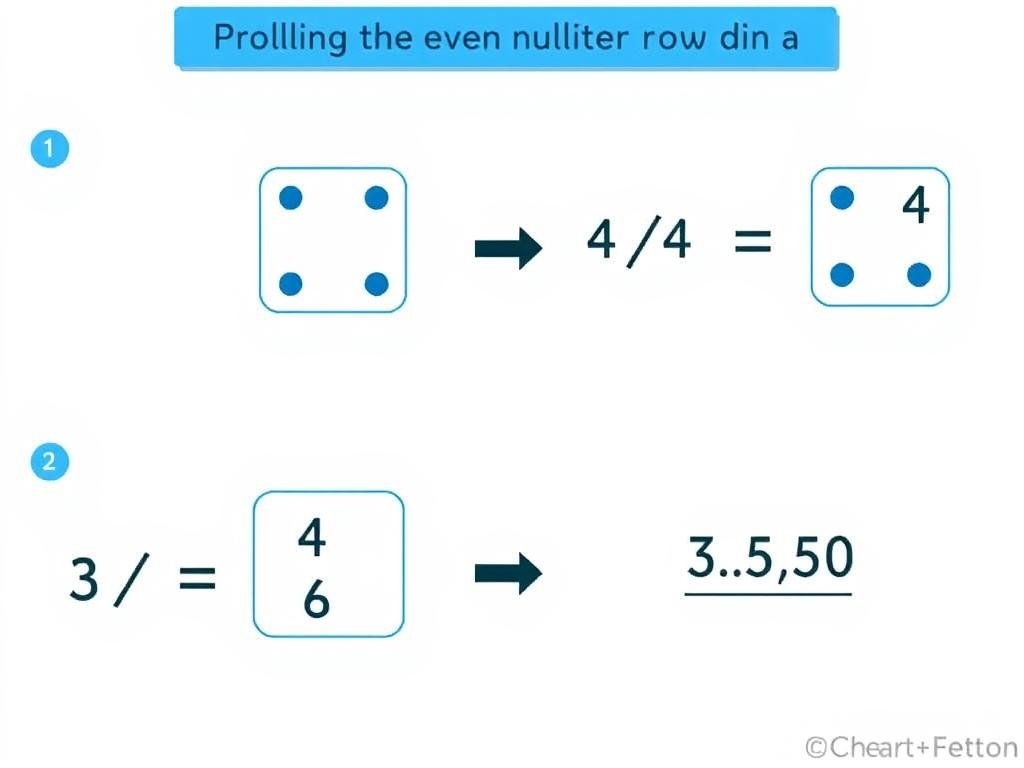
Problem: What is the probability of rolling an even number on a standard six-sided die?
Solution:
- Identify the favorable outcomes: Even numbers on a die are 2, 4, and 6, so there are 3 favorable outcomes.
- Identify the total possible outcomes: A standard die has 6 possible outcomes (1, 2, 3, 4, 5, 6).
- Apply the probability formula: P(even) = 3/6 = 0.5 or 50%.
Therefore, the probability of rolling an even number is 0.5 or 50%.
Example 2: Independent Events
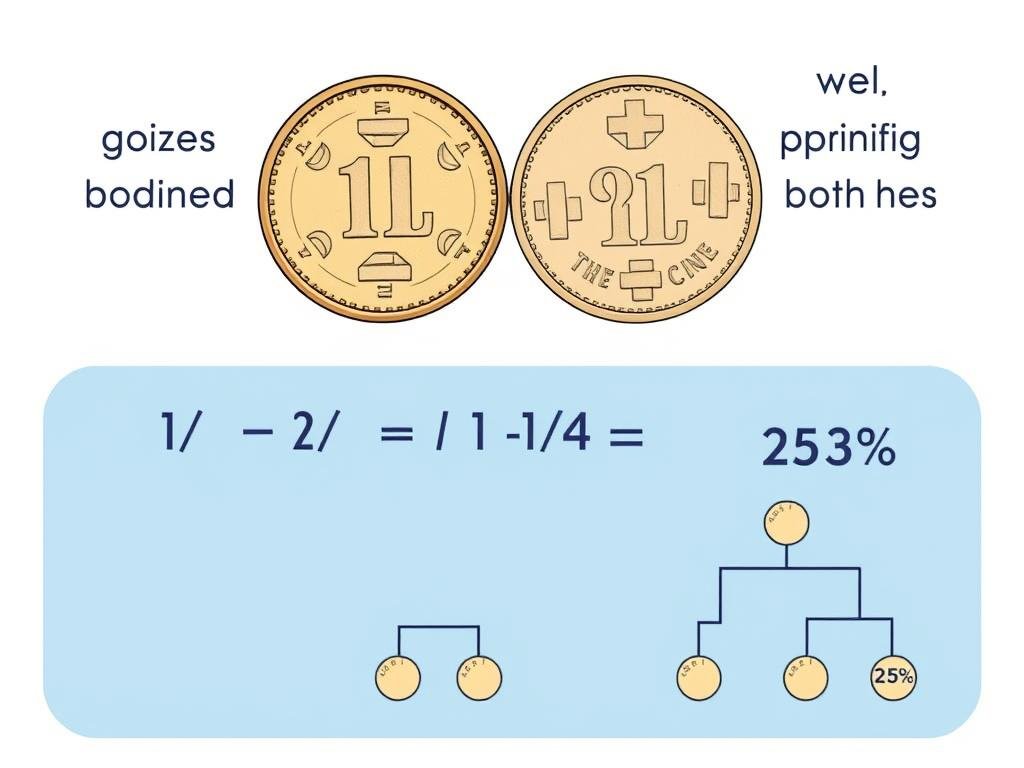
Problem: What is the probability of flipping a coin twice and getting heads both times?
Solution:
- Identify that these are independent events (first flip doesn’t affect second flip).
- Calculate probability of first event: P(heads on first flip) = 1/2 = 0.5.
- Calculate probability of second event: P(heads on second flip) = 1/2 = 0.5.
- Apply the multiplication rule for independent events: P(heads and heads) = 0.5 × 0.5 = 0.25 or 25%.
Therefore, the probability of getting heads on both flips is 0.25 or 25%.
Try These Examples Yourself
Use our probability calculator to verify these examples and solve your own probability problems.
Example 3: Conditional Probability

Problem: A bag contains 5 red marbles and 3 blue marbles. If you draw two marbles without replacement, what is the probability that the second marble is blue given that the first marble was red?
Solution:
- Calculate P(first marble is red): 5/8 = 0.625.
- After drawing a red marble, the bag contains 4 red marbles and 3 blue marbles.
- Calculate P(second marble is blue | first marble was red): 3/7 ≈ 0.429.
Therefore, the probability that the second marble is blue given that the first marble was red is approximately 0.429 or 42.9%.
Real-World Applications of Probability

Probability calculations are used across numerous fields and everyday situations:
Finance & Insurance
- Risk assessment for investments
- Insurance premium calculations
- Stock market analysis
- Portfolio diversification strategies
Science & Medicine
- Clinical trial analysis
- Genetic inheritance prediction
- Disease outbreak modeling
- Diagnostic test accuracy
Everyday Life
- Weather forecasting
- Sports analytics
- Quality control in manufacturing
- Games of chance
Case Study: Medical Testing

Consider a medical test for a disease that affects 1% of the population. The test is 95% accurate for both positive and negative results.
If someone tests positive, what’s the probability they actually have the disease?
Many people intuitively guess around 95%, but using Bayes’ theorem:
P(Disease|Positive) = [P(Positive|Disease) × P(Disease)] / P(Positive)
P(Disease|Positive) = [0.95 × 0.01] / [0.95 × 0.01 + 0.05 × 0.99]
P(Disease|Positive) ≈ 0.16 or 16%
This surprisingly low result demonstrates why understanding probability is crucial in interpreting test results and making informed decisions.
Solve Complex Probability Problems
Our probability calculator can help you work through real-world probability scenarios like these.
Understanding Probability Distributions

Probability distributions describe how the probabilities are distributed over the values of a random variable. Here are some common distributions:
Normal Distribution
Also known as the Gaussian distribution or bell curve, the normal distribution is symmetrical and defined by its mean and standard deviation. It’s commonly used to model natural phenomena and is the foundation of many statistical methods.
The probability density function for a normal distribution is:
f(x) = (1/σ√(2π)) × e^(-(x-μ)²/(2σ²))
Where μ is the mean and σ is the standard deviation.
Binomial Distribution
The binomial distribution models the number of successes in a fixed number of independent trials, each with the same probability of success. It’s used for yes/no questions or success/failure scenarios.
Poisson Distribution
The Poisson distribution models the number of events occurring in a fixed interval of time or space, assuming these events occur independently and at a constant average rate.
Our probability calculator can help you work with these distributions to find probabilities for specific values or ranges.
Common Probability Misconceptions

Many people misunderstand probability concepts, leading to poor decision-making. Here are some common misconceptions:
Correct Understanding
- Independent events remain independent regardless of past outcomes
- The probability of specific conditions is always less than or equal to the probability of more general conditions
- Rare coincidences are expected given enough opportunities
- Base rates must be considered when interpreting test results
Common Misconceptions
- The Gambler’s Fallacy: Believing that past outcomes affect future independent events
- The Conjunction Fallacy: Believing that specific conditions are more probable than general ones
- The Hot Hand Fallacy: Seeing patterns in truly random sequences
- Base Rate Neglect: Ignoring prior probabilities when assessing likelihood
Understanding these misconceptions can help you make better probability-based decisions in everyday life.
Frequently Asked Questions About Probability
What is the difference between theoretical and experimental probability?
Theoretical probability is calculated mathematically based on the possible outcomes, while experimental probability is determined by conducting experiments and observing the actual outcomes. For example, the theoretical probability of getting heads when flipping a fair coin is 0.5, but if you flip a coin 10 times and get 6 heads, the experimental probability would be 0.6.
How do I calculate the probability of mutually exclusive events?
For mutually exclusive events (events that cannot occur simultaneously), the probability of either event occurring is the sum of their individual probabilities: P(A or B) = P(A) + P(B). For example, the probability of rolling either a 1 or a 2 on a die is 1/6 + 1/6 = 2/6 = 1/3.
What does it mean when two events are independent?
Two events are independent when the occurrence of one event does not affect the probability of the other event. For example, when flipping a coin twice, getting heads on the first flip doesn’t change the probability of getting heads on the second flip.
How is conditional probability different from joint probability?
Conditional probability is the probability of an event occurring given that another event has already occurred, denoted as P(A|B). Joint probability is the probability of two events occurring together, denoted as P(A and B). They’re related by the formula: P(A and B) = P(B) × P(A|B).
Can a probability ever be greater than 1 or less than 0?
No, probabilities are always between 0 and 1, inclusive. A probability of 0 means the event is impossible, while a probability of 1 means the event is certain to occur. Any value in between represents the likelihood of the event happening.

Simplify Your Probability Calculations
Probability calculations can range from simple to highly complex, but understanding the fundamental concepts and formulas provides a solid foundation for tackling any probability problem. Whether you’re a student studying statistics, a professional analyzing data, or simply curious about the likelihood of events, our probability calculator can help you find accurate results quickly and easily.
By using our probability calculator, you can:
- Calculate single event probabilities
- Determine the likelihood of independent and dependent events
- Solve conditional probability problems
- Work with probability distributions
- Avoid common probability misconceptions
Ready to Calculate Probabilities?
Skip the complex formulas and get instant, accurate probability calculations for any scenario.