Pythagorean Theorem Calculator

The Pythagorean theorem is a fundamental mathematical principle that has shaped geometry for over 2,500 years. This powerful formula allows you to find unknown sides of right triangles, making it essential for students, educators, engineers, and anyone working with geometric calculations. Our Pythagorean theorem calculator simplifies this process, providing instant and accurate results for all your right triangle calculations.

What Is the Pythagorean Theorem?

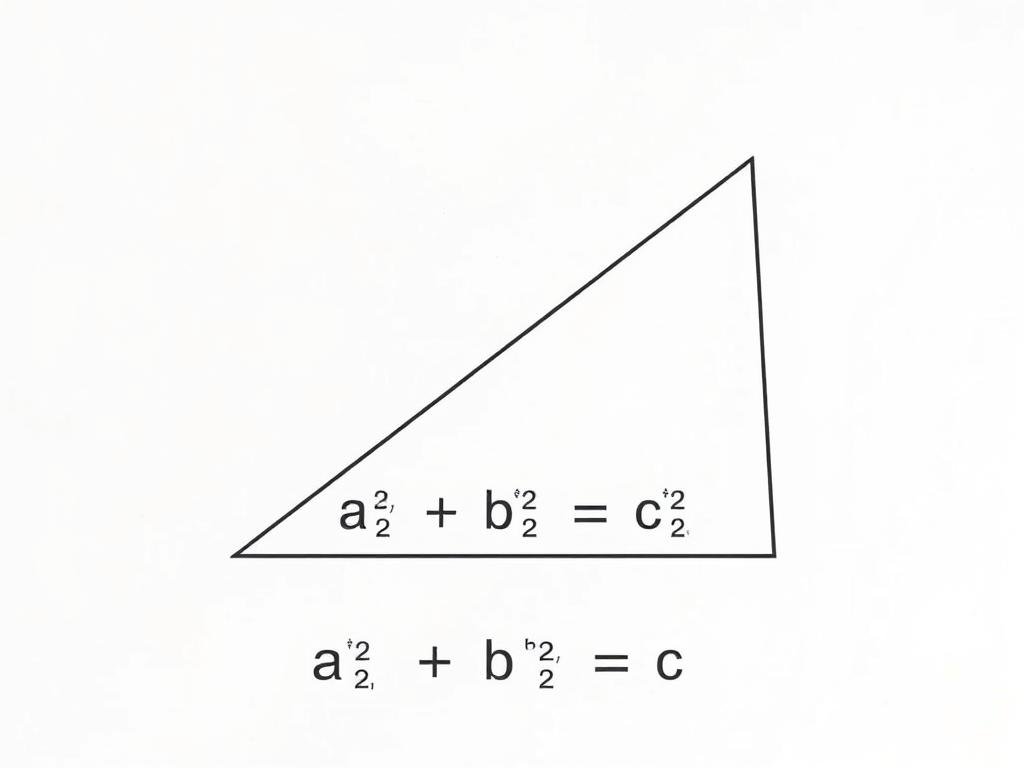
The Pythagorean theorem states that in any right triangle, the square of the length of the hypotenuse (the side opposite the right angle) equals the sum of squares of the other two sides (legs). This relationship is expressed in the famous equation:

Named after the ancient Greek mathematician Pythagoras (570-495 BCE), this theorem has become one of the most widely used mathematical principles. While Pythagoras is credited with the first proof, evidence suggests the relationship was known and used by Babylonian and Egyptian civilizations centuries earlier.

How to Use the Pythagorean Theorem

The Pythagorean theorem is versatile and can be used to find any side of a right triangle when you know the other two sides. Here’s how to apply it in different scenarios:

Finding the Hypotenuse (c)

When you know both legs (a and b) and need to find the hypotenuse (c):

1. Square both leg values (a² and b²)
2. Add these squared values together (a² + b²)
3. Take the square root of this sum to find c (c = √(a² + b²))

Finding a Leg (a or b)

When you know the hypotenuse (c) and one leg (either a or b) and need to find the other leg:

1. Square both the known values (c² and either a² or b²)
2. Subtract the squared leg from the squared hypotenuse (c² – a² or c² – b²)
3. Take the square root of this difference to find the unknown leg

Step-by-Step Calculation Examples

Example 1: Finding the Hypotenuse

Problem: A right triangle has legs of 3 units and 4 units. Find the hypotenuse.

Solution:

1. Identify the known values: a = 3, b = 4
2. Apply the Pythagorean theorem: c² = a² + b²
3. Substitute the values: c² = 3² + 4² = 9 + 16 = 25
4. Take the square root: c = √25 = 5

Answer: The hypotenuse is 5 units long.

Example 2: Finding a Leg

Problem: A right triangle has a hypotenuse of 10 units and one leg of 8 units. Find the other leg.

Solution:

1. Identify the known values: c = 10, a = 8
2. Rearrange the Pythagorean theorem to solve for b: b² = c² – a²
3. Substitute the values: b² = 10² – 8² = 100 – 64 = 36
4. Take the square root: b = √36 = 6

Answer: The missing leg is 6 units long.

Real-World Applications of the Pythagorean Theorem

The Pythagorean theorem extends far beyond classroom exercises, finding practical applications in numerous fields:

Construction & Architecture

• Ensuring corners are perfectly square in building construction
• Calculating diagonal distances across rooms
• Determining rafter lengths in roof construction
• Measuring diagonal bracing for structural stability

Navigation & Geography

• Calculating straight-line distances on maps
• Determining flight paths between locations
• Measuring distances across terrain
• GPS and navigation system calculations

Engineering & Physics

• Calculating resultant forces in physics
• Determining electrical impedance in circuits
• Measuring diagonal structural supports
• Calculating distances in 3D modeling

Practical Example: Ladder Placement

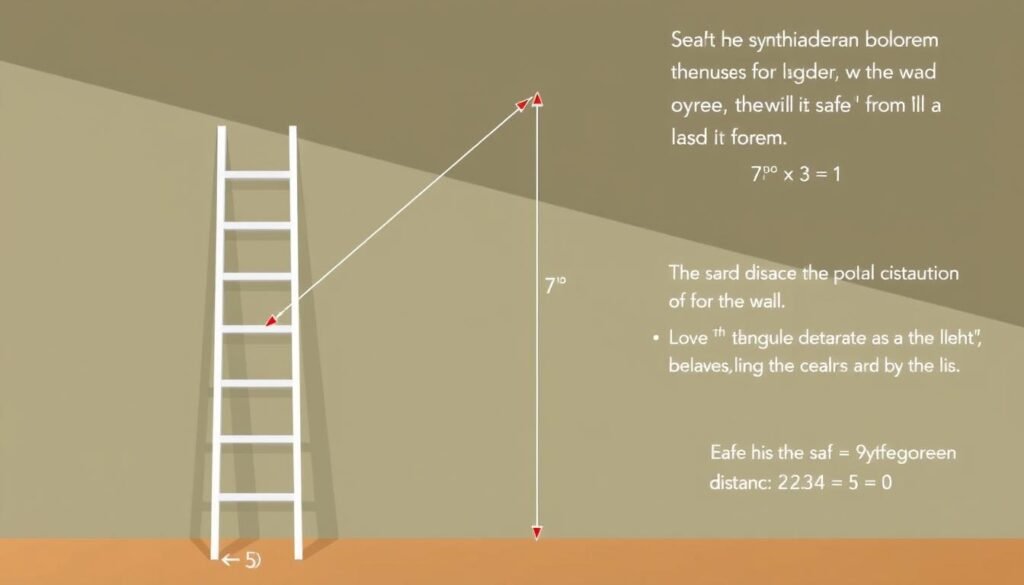
A 5-meter ladder needs to reach a height of 4 meters on a wall. How far should the base of the ladder be positioned from the wall for safe placement?

Solution:

1. The ladder length is the hypotenuse (c = 5 meters)
2. The height is one leg (a = 4 meters)
3. Using the Pythagorean theorem: b² = c² – a² = 5² – 4² = 25 – 16 = 9
4. Taking the square root: b = 3 meters

Answer: The ladder should be positioned 3 meters from the wall.

Common Mistakes to Avoid When Using the Pythagorean Theorem

Special Right Triangles and the Pythagorean Theorem

Certain right triangles have special properties that make calculations even simpler. Recognizing these patterns can save time and provide insights into geometric relationships.

3-4-5 Triangle

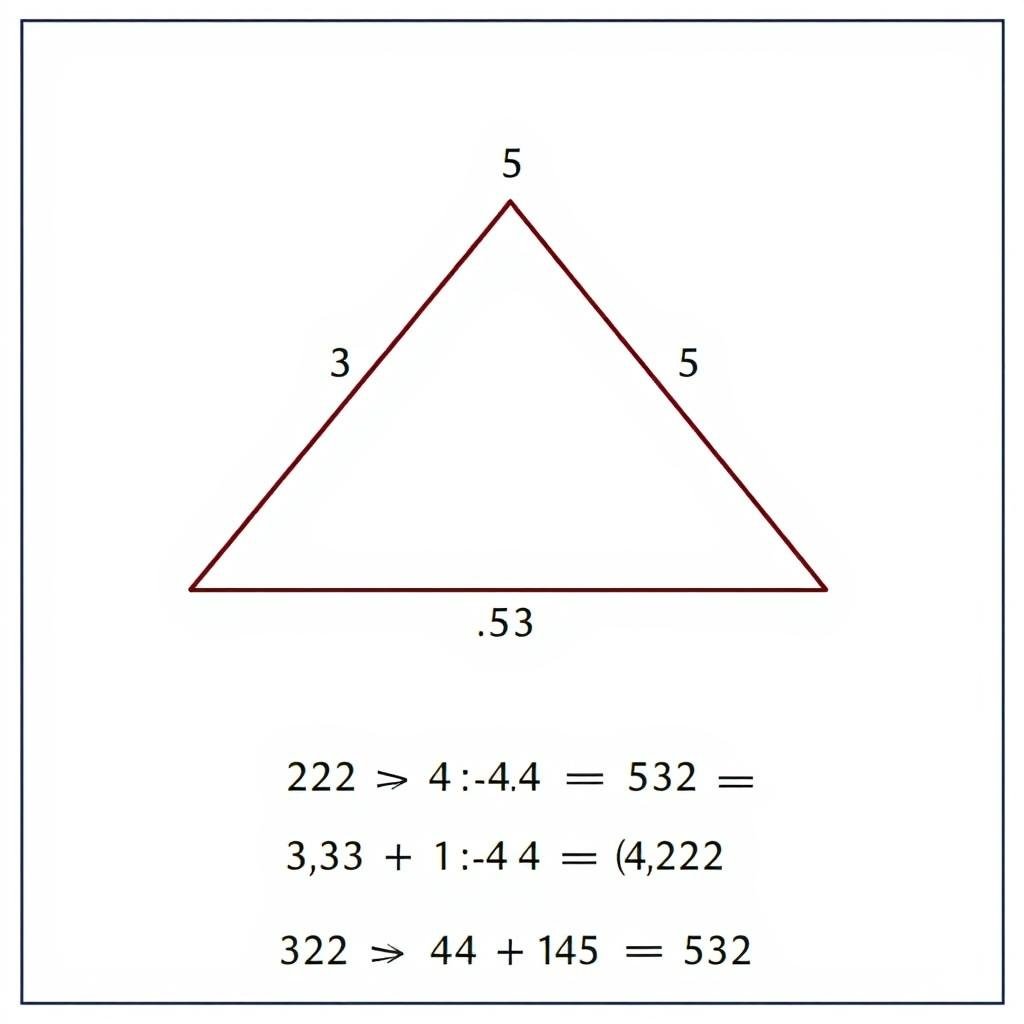
The 3-4-5 triangle is the simplest Pythagorean triple, where:

• 3² + 4² = 9 + 16 = 25 = 5²

Any triangle with sides in the ratio 3:4:5 is a right triangle. This pattern is commonly used in construction to ensure right angles.

45-45-90 Triangle (Isosceles Right Triangle)

In this special triangle:

• Both legs are equal in length
• If each leg has length a, the hypotenuse is a√2
• The angles are 45°, 45°, and 90°

30-60-90 Triangle

This triangle has special proportions:

• If the shortest leg has length a (opposite to the 30° angle)
• The other leg (opposite to the 60° angle) is a√3
• The hypotenuse is 2a

These relationships can be verified using the Pythagorean theorem: a² + (a√3)² = (2a)²

Conclusion: Mastering the Pythagorean Theorem

The Pythagorean theorem stands as one of mathematics’ most elegant and practical formulas. From ancient civilizations to modern technology, this simple relationship between the sides of a right triangle continues to be an essential tool in countless applications.

Whether you’re a student learning geometry, a professional in construction or engineering, or simply someone who appreciates the beauty of mathematical relationships, understanding the Pythagorean theorem opens doors to solving a wide range of practical problems.

While manual calculations using the theorem are straightforward, our Pythagorean theorem calculator offers a quick, accurate way to find missing sides of right triangles without the potential for calculation errors. It’s a valuable tool that saves time while ensuring precision in all your geometric calculations.