Struggling with quadratic equations? You’re not alone. Whether you’re a student tackling algebra homework or a professional using mathematical models, the quadratic formula is an essential tool in your mathematical toolkit. This comprehensive guide explains everything you need to know about the quadratic formula, how to use it effectively, and why our Quadratic Formula Calculator makes solving these equations faster and more accurate than ever.
What is the Quadratic Formula?
The quadratic formula is a mathematical solution for finding the roots of any quadratic equation. It works by expressing the solutions in terms of the coefficients of the equation.

The quadratic formula with each component labeled
For any quadratic equation in the standard form ax² + bx + c = 0, the quadratic formula gives us the solutions:
Where:
- a is the coefficient of x² (cannot be zero)
- b is the coefficient of x
- c is the constant term
- The expression b² – 4ac is called the discriminant
Need a Quick Solution?
Skip the manual calculations and get instant, accurate results for any quadratic equation.
Understanding the Standard Form
Before applying the quadratic formula, you must express your equation in the standard form: ax² + bx + c = 0. This means moving all terms to one side of the equation, with zero on the other side.
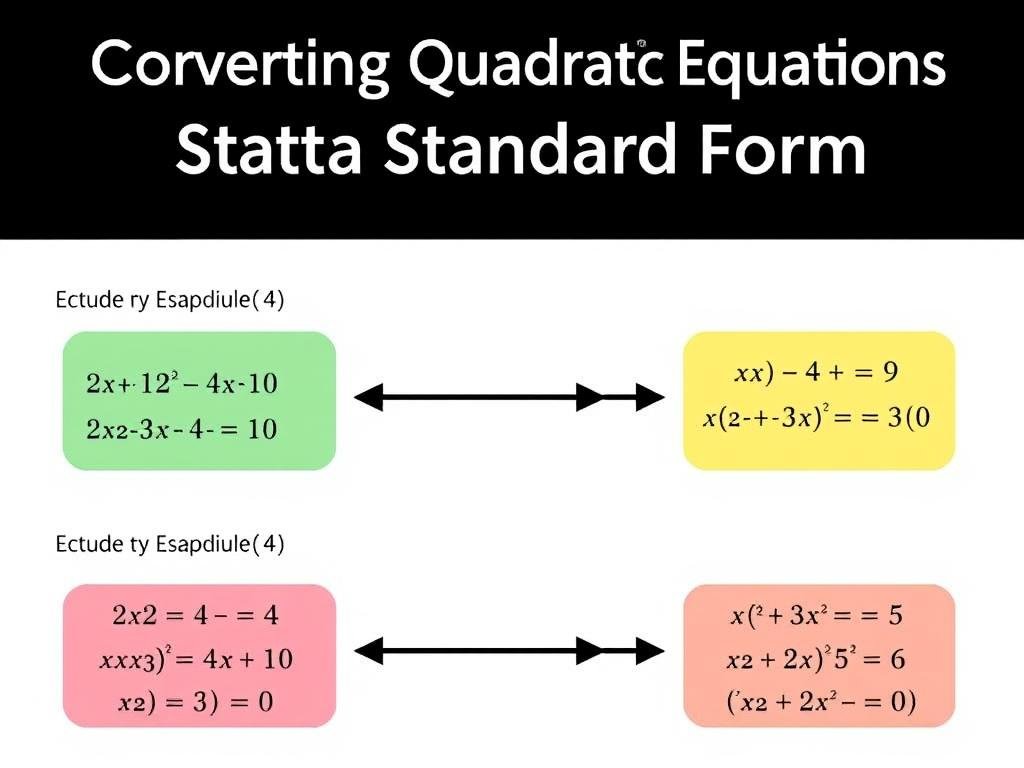
Common mistake: Not setting the equation to zero
One of the most common errors when solving quadratic equations is trying to apply the formula without first moving all terms to one side. For example, with x² + 5x = 6, you must first rewrite it as x² + 5x – 6 = 0 before identifying a=1, b=5, and c=-6.
How to Use the Quadratic Formula: Step-by-Step Guide
Solving quadratic equations using the formula involves a systematic approach. Let’s walk through an example to demonstrate the process.
Example Problem: Solve 2x² – 7x + 3 = 0

- Identify the coefficients:
- a = 2 (coefficient of x²)
- b = -7 (coefficient of x)
- c = 3 (constant term)
- Calculate the discriminant:
- Discriminant = b² – 4ac
- = (-7)² – 4(2)(3)
- = 49 – 24
- = 25
- Apply the quadratic formula:
- x = (-b ± √(discriminant))/2a
- x = (7 ± √25)/4
- x = (7 ± 5)/4
- Calculate both solutions:
- x₁ = (7 + 5)/4 = 12/4 = 3
- x₂ = (7 – 5)/4 = 2/4 = 0.5
Therefore, the solutions to 2x² – 7x + 3 = 0 are x = 3 and x = 0.5.
Save Time on Calculations
Get instant solutions to any quadratic equation without going through all these steps manually.
Understanding the Discriminant
The discriminant (b² – 4ac) is a crucial part of the quadratic formula that tells you important information about the solutions before you even solve the equation.

How the discriminant determines the nature of solutions
Discriminant > 0
The equation has two distinct real solutions. The parabola crosses the x-axis at two points.
Discriminant = 0
The equation has exactly one real solution (a repeated root). The parabola touches the x-axis at exactly one point.
Discriminant
The equation has no real solutions, but two complex solutions. The parabola doesn’t intersect the x-axis.
Quick Tip: The discriminant can save you time! Before solving the entire equation, calculate b² – 4ac to determine what type of solutions to expect.
Different Methods for Solving Quadratic Equations
While the quadratic formula is universal, there are several other methods for solving quadratic equations, each with its own advantages in specific situations.

| Method | Best Used When | Advantages | Limitations |
| Factoring | Equation can be easily factored | Quick and straightforward | Not all equations can be factored easily |
| Completing the Square | Converting to vertex form is helpful | Works for all quadratics; helps understand the graph | Can be tedious with complex numbers |
| Quadratic Formula | Equation is complex or has decimal coefficients | Works for all quadratics; direct formula | More calculation steps than factoring |
| Graphical Method | Visual understanding is needed | Provides visual insight into solutions | May not give exact values; requires graphing tools |
Not Sure Which Method to Use?
Our calculator handles all the complexity for you, choosing the most efficient method automatically.
Real-World Applications of Quadratic Equations
Quadratic equations aren’t just classroom exercises—they have numerous practical applications across various fields.
Quadratic equations in everyday life and professional fields
Physics and Engineering
- Projectile Motion: The path of an object thrown into the air follows a parabolic trajectory described by quadratic equations.
- Optics: The shape of parabolic mirrors and lenses, used in telescopes and satellite dishes, is based on quadratic functions.
- Architecture: Suspension bridges often use cables in parabolic shapes that can be modeled with quadratic equations.
Economics and Business
- Profit Optimization: Finding the maximum profit or minimum cost often involves solving quadratic equations.
- Supply and Demand: Some economic models use quadratic equations to describe market equilibrium.
- Revenue Forecasting: Predicting diminishing returns in sales and marketing can involve quadratic models.
Example: Using quadratic equations to calculate when a thrown ball will hit the ground
Why Use a Quadratic Formula Calculator?
While understanding how to solve quadratic equations manually is important, using a dedicated calculator offers numerous advantages.
Benefits of Using Our Calculator
- Speed: Get instant results without manual calculations
- Accuracy: Eliminate human error in complex calculations
- Versatility: Solve any quadratic equation, including those with complex solutions
- Educational Value: See step-by-step solutions to understand the process
- Time-Saving: Focus on understanding concepts rather than calculation mechanics
Limitations of Manual Calculations
- Time-Consuming: Manual calculations take longer, especially with complex numbers
- Error-Prone: Easy to make arithmetic mistakes with complex formulas
- Limited Verification: Harder to check your work without a second calculation
- Difficult with Decimals: Calculations become tedious with non-integer coefficients
- Challenging for Complex Roots: Manual work with complex numbers is more error-prone
Experience the Difference
Join thousands of students and professionals who save time and get accurate results with our calculator.
Common Mistakes When Solving Quadratic Equations
Even with a good understanding of the quadratic formula, it’s easy to make errors. Here are some common mistakes to avoid:

Misidentifying the coefficients
Always make sure your equation is in standard form (ax² + bx + c = 0) before identifying a, b, and c. For example, in 3x² – 2x + 5 = 0, a=3, b=-2, and c=5.
Sign errors
Be careful with negative signs, especially in the formula. Remember that -b means the opposite of b, so if b is already negative, -b will be positive.
Calculation errors in the discriminant
Double-check your calculation of b² – 4ac. A small error here can completely change your solutions.
Forgetting the ± in the formula
The quadratic formula gives two solutions: one with + √(b² – 4ac) and one with – √(b² – 4ac). Don’t forget to calculate both.
Conclusion: Mastering Quadratic Equations
Understanding the quadratic formula is an essential skill in algebra that opens doors to solving a wide range of mathematical problems. While manual calculation is valuable for learning, our Quadratic Formula Calculator provides a reliable, accurate, and time-saving alternative for students, educators, and professionals alike.
Whether you’re working on homework, preparing for an exam, or applying mathematical concepts in your professional field, having a reliable tool to solve quadratic equations quickly can make a significant difference in your efficiency and accuracy.
Ready to Solve Your Quadratic Equations?
Use our dedicated Quadratic Formula Calculator for instant, accurate results every time.