Roots are fundamental mathematical operations that appear in countless equations, formulas, and real-world applications. Whether you’re solving a quadratic equation, calculating dimensions, or working on advanced mathematical problems, finding roots accurately is essential. Our Root Calculator provides a simple yet powerful solution for calculating square roots, cube roots, and nth roots with precision and ease.
Need Quick & Accurate Root Calculations?
Stop struggling with complex manual calculations. Our Root Calculator delivers instant, precise results for any root calculation.
What Are Mathematical Roots?
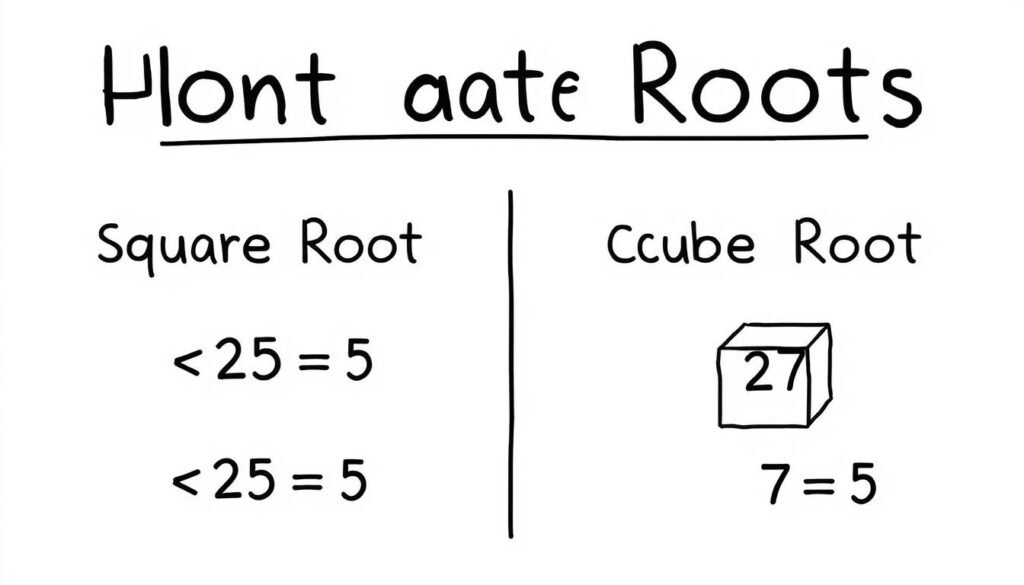
Visual representation of square root and cube root operations
In mathematics, a root of a number is a value that, when multiplied by itself a certain number of times, gives the original number. The most common type is the square root, where a number multiplied by itself equals the original value.
For example, the square root of 25 is 5, because 5 × 5 = 25. Similarly, the cube root of 27 is 3, because 3 × 3 × 3 = 27. This concept extends to any nth root, where a value raised to the power of n equals the original number.
Roots are represented using the radical symbol (√) with an optional index number indicating the type of root:
- Square root: √x or ²√x
- Cube root: ³√x
- Fourth root: ⁴√x
- Nth root: ⁿ√x
Understanding roots is crucial for solving equations, particularly when dealing with variables raised to powers. They help us find unknown values and are essential in fields ranging from algebra to calculus and beyond.
Types of Roots in Mathematics

Square Roots
The most common type of root, represented as √x. A square root of a number gives a value that, when multiplied by itself, equals the original number.
Example: √16 = 4 because 4² = 16

Cube Roots
Represented as ³√x or ∛x. A cube root of a number gives a value that, when cubed (raised to the power of 3), equals the original number.
Example: ∛27 = 3 because 3³ = 27

Nth Roots
Represented as ⁿ√x. An nth root of a number gives a value that, when raised to the power of n, equals the original number.
Example: ⁴√16 = 2 because 2⁴ = 16
Calculate Any Root Instantly
From simple square roots to complex nth roots, our calculator handles them all with precision.
Mathematical Formulas for Root Calculations

Essential formulas for calculating various types of roots
Understanding the mathematical formulas behind root calculations helps in solving problems manually and appreciating how root calculators work. Here are the key formulas:
Basic Root Formulas
- Square Root: √x = x^(1/2)
- Cube Root: ∛x = x^(1/3)
- Nth Root: ⁿ√x = x^(1/n)
Finding Roots of Equations
When solving equations, roots often represent the values of variables that make the equation true. For quadratic equations in the form ax² + bx + c = 0, the roots can be found using the quadratic formula:

For higher-degree polynomials, finding roots becomes more complex and often requires numerical methods or specialized calculators.
Properties of Roots
- Product Rule: √(a × b) = √a × √b (where a, b ≥ 0)
- Quotient Rule: √(a ÷ b) = √a ÷ √b (where a ≥ 0, b > 0)
- Power Rule: √(a^n) = (√a)^n (where a ≥ 0)
These properties are fundamental when simplifying expressions containing roots and are built into advanced root calculators for efficient computation.
Step-by-Step Root Calculation Examples
Example 1: Finding a Square Root
Let’s calculate √49 manually:
- Identify the perfect squares closest to 49: 36 (6²) and 64 (8²)
- Since 49 is a perfect square (7²), the square root is exactly 7
- Therefore, √49 = 7

Example 2: Finding a Cube Root
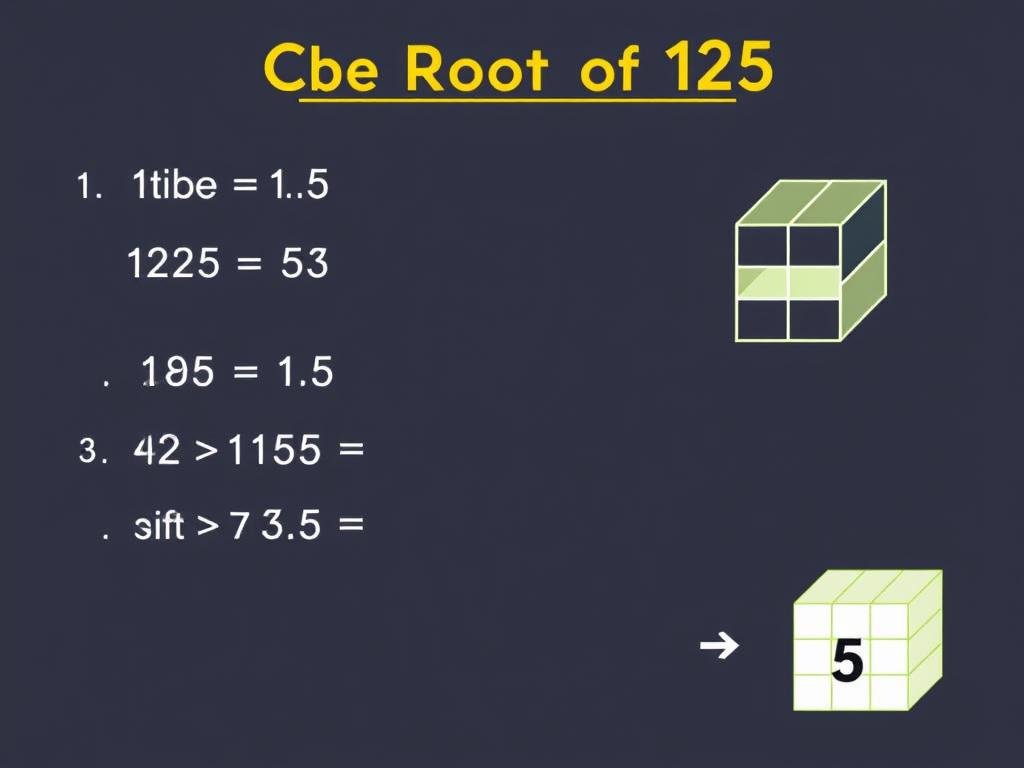
Let’s calculate ∛125 manually:
- Identify the perfect cubes closest to 125: 64 (4³) and 125 (5³)
- Since 125 is a perfect cube (5³), the cube root is exactly 5
- Therefore, ∛125 = 5
Example 3: Using the Quadratic Formula to Find Roots
Let’s solve the quadratic equation x² – 5x + 6 = 0:
- Identify the values: a = 1, b = -5, c = 6
- Apply the quadratic formula: x = (-b ± √(b² – 4ac))/2a
- Substitute the values: x = (5 ± √(25 – 24))/2
- Simplify: x = (5 ± √1)/2
- Calculate the roots: x = (5 + 1)/2 = 3 or x = (5 – 1)/2 = 2
- Therefore, the roots are x = 2 and x = 3

Step-by-step application of the quadratic formula
Manual calculations can be time-consuming and prone to errors, especially with complex numbers or non-perfect roots. Using a dedicated root calculator ensures accuracy and saves valuable time.
Skip the Manual Calculations
Get instant, accurate results for any root calculation with our specialized calculator.
Real-World Applications of Root Calculations

Root calculations are essential in numerous practical applications
Root calculations extend far beyond academic exercises, playing crucial roles in various real-world scenarios:
Engineering & Architecture
- Calculating structural stability
- Determining dimensions and proportions
- Analyzing vibration frequencies
- Computing stress and strain relationships
Finance & Economics
- Calculating compound interest
- Determining growth rates
- Computing investment returns
- Analyzing economic models
Science & Technology
- Physics equations (e.g., pendulum period)
- Signal processing algorithms
- Computer graphics rendering
- Statistical analysis and modeling
Case Study: The Pythagorean Theorem

The Pythagorean theorem relies on square root calculations
One of the most common applications of square roots is in the Pythagorean theorem (a² + b² = c²), which is used to find the length of a right triangle’s hypotenuse. This has countless practical applications:
- Surveyors determining distances and areas
- Navigation systems calculating the shortest path
- Construction workers ensuring right angles and proper dimensions
- GPS technology computing distances between coordinates
In each of these cases, accurate root calculations are essential for precise results, highlighting the importance of reliable root calculators in professional applications.
Benefits of Using a Root Calculator
Advantages of Digital Root Calculators
- Instant results for any type of root calculation
- Perfect accuracy even with complex or irrational roots
- Ability to handle large numbers without approximation errors
- Time-saving for students, professionals, and researchers
- Elimination of manual calculation errors
- Support for advanced mathematical operations
- Accessibility on multiple devices
Limitations of Manual Calculations
- Time-consuming, especially for complex roots
- Prone to human error in calculation steps
- Difficult to achieve high precision with irrational roots
- Requires memorization of formulas and properties
- Challenging for non-perfect roots without a calculator
- Impractical for rapid calculations in professional settings
Digital calculators offer significant advantages over manual methods
“The development of digital root calculators has revolutionized how we approach mathematical problems, allowing students and professionals to focus on understanding concepts rather than getting lost in tedious calculations.”
Experience the Benefits Yourself
Join thousands of students, educators, and professionals who rely on our Root Calculator for fast, accurate results.
Common Challenges in Root Calculations

Understanding common pitfalls helps avoid calculation errors
Challenge 1: Dealing with Negative Numbers
One of the most common challenges is understanding how to handle negative numbers in root calculations. For example, √(-9) doesn’t have a real number solution because no real number squared equals -9. However, in the complex number system, √(-9) = 3i, where i is the imaginary unit.
Challenge 2: Simplifying Radical Expressions
Simplifying expressions containing roots can be tricky, especially when dealing with non-perfect roots. For example, simplifying √12 requires recognizing that √12 = √(4 × 3) = √4 × √3 = 2√3.
Challenge 3: Rationalizing Denominators
When a root appears in the denominator of a fraction, it’s often necessary to rationalize it by multiplying both numerator and denominator by the same root. For example, 1/√2 can be rationalized to √2/2 by multiplying both top and bottom by √2.
Challenge 4: Working with Decimal Approximations
Many roots result in irrational numbers that can only be approximated as decimals. For instance, √2 ≈ 1.414213562… This can lead to rounding errors in manual calculations.
Pro Tip: Our Root Calculator handles all these challenges automatically, providing exact symbolic answers when possible and high-precision decimal approximations when needed.
Proper techniques for overcoming common root calculation challenges
Frequently Asked Questions About Root Calculations
What is the difference between a square root and a cube root?
A square root (√x) is a value that, when multiplied by itself, equals the original number. For example, √9 = 3 because 3 × 3 = 9. A cube root (∛x) is a value that, when cubed (raised to the power of 3), equals the original number. For example, ∛27 = 3 because 3³ = 27.
Can negative numbers have square roots?
In the real number system, negative numbers do not have square roots because no real number squared can equal a negative number. However, in the complex number system, negative numbers do have square roots. For example, √(-4) = 2i, where i is the imaginary unit.
How do I calculate the square root of a non-perfect square?
For non-perfect squares, you can use approximation methods like the Newton-Raphson method or decimal approximation. However, the most accurate and efficient approach is to use a root calculator, which can provide both exact symbolic forms and decimal approximations.
What are the applications of root calculations in real life?
Root calculations have numerous real-life applications, including engineering (structural analysis, electrical circuits), finance (compound interest, growth rates), physics (wave equations, gravitational formulas), computer graphics (rendering algorithms), and everyday measurements (using the Pythagorean theorem to calculate distances).
How accurate is an online root calculator?
High-quality online root calculators like ours provide extremely accurate results, often with precision to many decimal places. For exact roots (like √4 = 2), they provide the exact value. For irrational roots (like √2), they can provide both the exact symbolic form and a decimal approximation with the desired precision.
Visual guide to frequently asked questions about roots
Why Choose Our Root Calculator

Finding roots accurately and efficiently is essential for students, educators, engineers, financial analysts, and anyone working with mathematical calculations. Our Root Calculator offers the perfect solution with these key advantages:
Accuracy & Precision
Get exact results for any type of root calculation, from simple square roots to complex nth roots, with perfect precision every time.
Time-Saving Efficiency
Eliminate tedious manual calculations and get instant results, allowing you to focus on understanding concepts and solving problems.
Versatility & Flexibility
Calculate any type of root for any number, with support for square roots, cube roots, nth roots, and roots in equations.
Ready to Simplify Your Root Calculations?
Join thousands of satisfied users who rely on our Root Calculator for fast, accurate results.
Whether you’re a student tackling algebra problems, an educator preparing lesson materials, or a professional requiring precise calculations, our Root Calculator provides the reliability and convenience you need. Experience the difference that a specialized tool can make in your mathematical work.