Slope Calculator helps you quickly find the slope of a line using coordinates or equations. Accurate, easy, and ideal for math and geometry problems.
Slope Calculator
Understanding how to calculate the slope of a line is essential in mathematics, engineering, construction, and many other fields. Whether you’re a student working on homework, an engineer designing a road, or a construction professional planning a project, our comprehensive guide will help you master slope calculations. Read on to learn everything about slope formulas, step-by-step calculation methods, and why our free Slope Calculator tool can save you time and ensure accuracy.
What is Slope?
Slope is a mathematical measure of the steepness, incline, or grade of a line. In simple terms, it tells you how much a line rises or falls as it moves from left to right. The concept of slope is fundamental in mathematics and has numerous real-world applications in fields like engineering, physics, economics, and construction.
The slope of a line is often represented by the letter “m” and is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. This ratio gives us a numerical value that indicates both the direction and steepness of the line.
A positive slope means the line rises as it moves from left to right, while a negative slope indicates the line falls. The greater the absolute value of the slope, the steeper the line.
The Slope Formula
The standard formula for calculating the slope of a line between two points is:
m = (y₂ – y₁) / (x₂ – x₁)
Where:
- (x₁, y₁) are the coordinates of the first point
- (x₂, y₂) are the coordinates of the second point
- m is the slope of the line
This formula is also commonly referred to as “rise over run,” where:
- Rise = y₂ – y₁ (the vertical change)
- Run = x₂ – x₁ (the horizontal change)

Step-by-Step Guide to Calculate Slope
Follow these simple steps to manually calculate the slope between two points:
Example Calculation
Let’s calculate the slope of a line passing through the points (2, 3) and (6, 11):

Step 1: Identify the points
Point 1: (2, 3)
Point 2: (6, 11)
Step 2: Calculate the rise
y₂ – y₁ = 11 – 3 = 8
Step 3: Calculate the run
x₂ – x₁ = 6 – 2 = 4
Step 4: Divide rise by run
m = 8 ÷ 4 = 2
The slope of the line is 2, which means that for every 1 unit the line moves horizontally, it rises 2 units vertically.
Save Time with Our Slope Calculator
Why calculate manually when you can get instant, accurate results?
Types of Slope
There are four main types of slopes in mathematics, each with distinct characteristics:
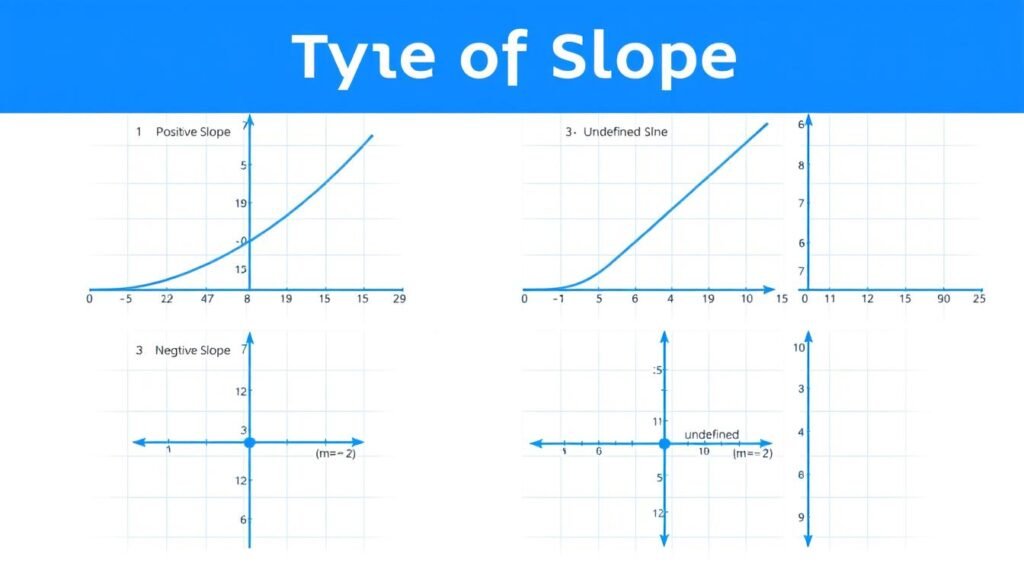
Positive Slope
A line with a positive slope rises from left to right. The greater the value, the steeper the incline.
Example: m = 2
Negative Slope
A line with a negative slope falls from left to right. The lower the value, the steeper the decline.
Example: m = -3
Zero Slope
A horizontal line has a slope of zero. There is no vertical change as x increases.
Example: m = 0
Undefined Slope
A vertical line has an undefined slope because the run equals zero, and division by zero is undefined.
Example: x = 5
Important Slope Equations
Beyond the basic slope formula, there are several important equations involving slope that are commonly used in mathematics:
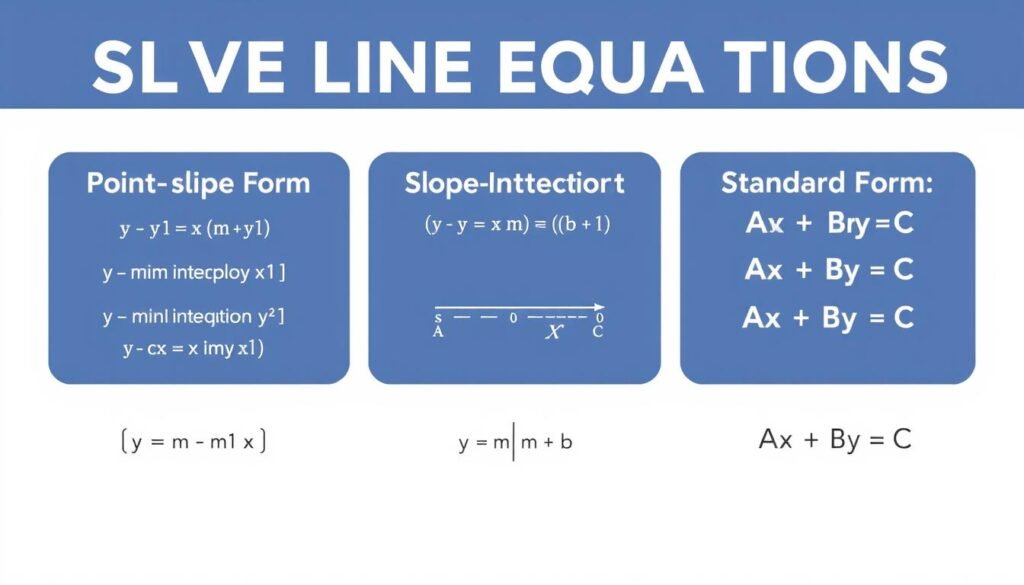
Point-Slope Form
y – y₁ = m(x – x₁)
This form is useful when you know the slope and a point on the line.
Slope-Intercept Form
y = mx + b
Where m is the slope and b is the y-intercept (where the line crosses the y-axis).
Standard Form
Ax + By = C
Where A, B, and C are constants, and A and B are not both zero.
Understanding these different forms allows you to work with linear equations more effectively and convert between different representations as needed.
Real-World Applications of Slope
The concept of slope extends far beyond mathematics textbooks and has numerous practical applications in various fields:
Engineering & Construction
- Designing roof pitches for proper drainage
- Building foundations on uneven terrain
- Creating proper drainage systems
- Designing retaining walls
Transportation
- Designing road grades for safety
- Railway track gradients
- Wheelchair ramp accessibility (ADA requires specific slopes)
- Airport runway design
Other Fields
- Economics: rate of change in graphs
- Physics: calculating velocity and acceleration
- Statistics: regression line analysis
- Geography: terrain analysis and mapping
Did you know? The steepest residential street in the world is Baldwin Street in New Zealand, with a maximum slope of approximately 35%, which corresponds to an angle of about 19 degrees!
Slope as Percentage and Angle
Slope can be expressed in different ways depending on the application:
Slope as a Ratio
The standard mathematical form: rise/run
Example: A slope of 0.5 means the line rises 1 unit for every 2 units of horizontal distance.
Slope as a Percentage
Calculated as: (rise/run) × 100%
Example: A slope of 0.5 equals a 50% grade, commonly used in road signs.
Slope as an Angle
Calculated as: θ = arctan(rise/run)
Example: A slope of 1 equals a 45° angle with the horizontal.
| Slope (Ratio) | Percentage | Angle (Degrees) | Common Application |
| 0.1 | 10% | 5.7° | Moderate road grade |
| 0.25 | 25% | 14° | Steep driveway |
| 0.5 | 50% | 26.6° | Steep hiking trail |
| 1 | 100% | 45° | Very steep slope |
Why Use an Online Slope Calculator?
- Instant results without manual calculation
- Eliminates human error in calculations
- Handles complex numbers and fractions easily
- Converts between different slope representations (ratio, percentage, angle)
- Saves time for students and professionals
- Provides additional line equation forms automatically
- Works on any device with internet access
Benefits of Using Our Slope Calculator
Whether you’re a student working on homework, an engineer designing a structure, or a construction professional planning a project, our Slope Calculator provides the accuracy and convenience you need for your calculations.
Ready to Calculate Slope Effortlessly?
Our free online Slope Calculator gives you instant, accurate results for any two points.
Frequently Asked Questions About Slope
What does a negative slope mean?
A negative slope indicates that the line decreases as it moves from left to right on a graph. In practical terms, this might represent a downhill grade, a decreasing relationship between variables, or a declining trend.
How do I find the slope of a vertical line?
A vertical line has an undefined slope because its run (horizontal change) is zero, and division by zero is undefined. Vertical lines are represented by equations of the form x = a, where a is a constant.
What’s the difference between slope and gradient?
In mathematics, “slope” and “gradient” are often used interchangeably to refer to the steepness of a line. However, in some contexts, particularly in engineering and geography, “gradient” may specifically refer to the slope expressed as a percentage or ratio.
How do I find the slope from a graph?
To find the slope from a graph, select any two points on the line, record their coordinates, and apply the slope formula: m = (y₂ – y₁) / (x₂ – x₁). For the most accurate results, choose points that fall exactly on grid intersections.

Master Slope Calculations with Our Free Tool
Understanding slope is fundamental to many mathematical concepts and real-world applications. Whether you’re calculating the grade of a road, analyzing data trends, or solving equations in algebra class, the ability to find and interpret slope is an essential skill.
Our free Slope Calculator makes this process quick, easy, and error-free. Instead of manually working through the calculations, you can get instant results and focus on applying the concepts to solve your problems.
Calculate Slope in Seconds
Stop struggling with manual calculations. Get precise results instantly with our free online tool.