Triangle Calculator

A triangle calculator is a powerful mathematical tool designed to solve various triangle problems with precision and ease. Whether you’re a student tackling geometry homework, an engineer working on structural designs, or a professional needing quick and accurate calculations, our triangle calculator provides comprehensive solutions for all triangle-related calculations. This guide explains everything you need to know about triangles and how our calculator can simplify complex mathematical operations.

What is a Triangle Calculator?

A triangle calculator is a specialized tool that helps determine unknown values of a triangle based on the information you provide. By entering known measurements such as sides, angles, area, or height, the calculator applies geometric principles and trigonometric formulas to compute the missing values. This eliminates the need for manual calculations and reduces the possibility of errors.

The calculator can handle various triangle types and calculation methods, including:

• SSS (Side-Side-Side): When all three sides are known
• SAS (Side-Angle-Side): When two sides and the included angle are known
• ASA (Angle-Side-Angle): When two angles and the included side are known
• AAS (Angle-Angle-Side): When two angles and a non-included side are known
• SSA (Side-Side-Angle): When two sides and a non-included angle are known

Understanding Triangle Properties

Before diving into calculations, it’s essential to understand the fundamental properties of triangles. A triangle is a polygon with three sides, three vertices, and three internal angles that sum to 180 degrees (or π radians).

Basic Triangle Components

Sides: Every triangle has three sides, typically denoted as a, b, and c. The side opposite to angle A is labeled as a, the side opposite to angle B is labeled as b, and the side opposite to angle C is labeled as c.

Angles: The three internal angles of a triangle are usually denoted as A, B, and C (or α, β, and γ). These angles always sum to 180 degrees.

Derived Properties

From these basic components, we can derive several important properties:

• Perimeter: The sum of all three sides (a + b + c)
• Semi-perimeter (s): Half of the perimeter, calculated as s = (a + b + c)/2
• Area: Can be calculated using various formulas depending on the known values
• Heights (Altitudes): The perpendicular distances from each vertex to the opposite side
• Medians: Line segments connecting each vertex to the midpoint of the opposite side
• Angle Bisectors: Lines that divide each angle into two equal parts

Types of Triangles

Triangles can be classified based on their sides or angles. Understanding these classifications helps in applying the appropriate formulas for calculations.

Classification Based on Sides

Classification Based on Angles

Essential Triangle Formulas

Depending on the information available, different formulas can be used to calculate triangle properties. Here are some of the most important formulas used in our triangle calculator:

Area Formulas

Basic formula: Area = ½ × base × height

Heron’s formula: Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter

Using two sides and the included angle: Area = ½ × a × b × sin(C)

The Pythagorean Theorem

For right triangles, the Pythagorean theorem states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides:

c² = a² + b², where c is the hypotenuse

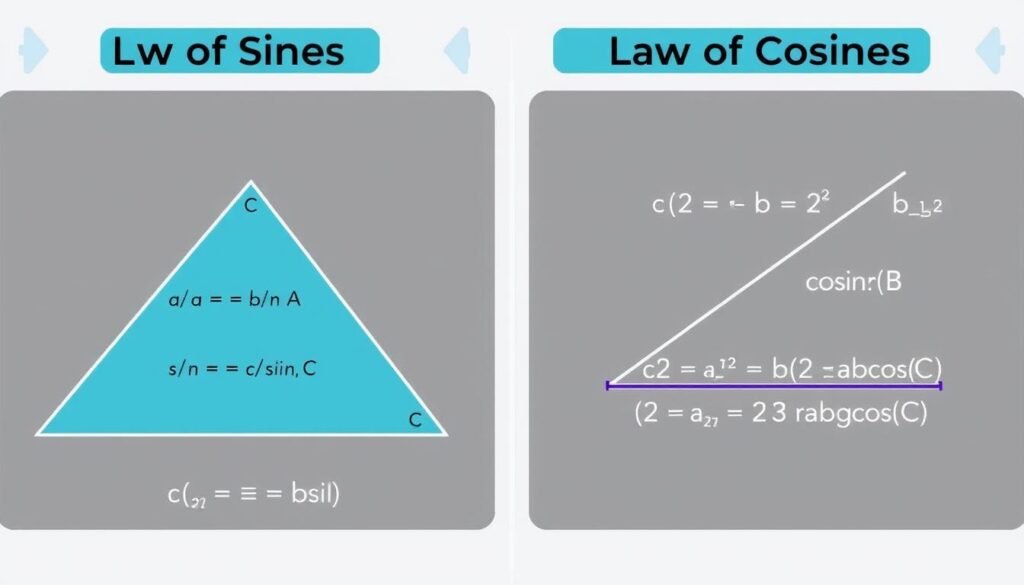
Law of Sines

The law of sines establishes the relationship between the sides of a triangle and the sines of the opposite angles:

a/sin(A) = b/sin(B) = c/sin(C)

This formula is particularly useful when solving triangles using the ASA, AAS, or SSA methods.

Law of Cosines

The law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles:

c² = a² + b² – 2ab × cos(C)

a² = b² + c² – 2bc × cos(A)

b² = a² + c² – 2ac × cos(B)

This formula is essential when solving triangles using the SSS or SAS methods.

Step-by-Step Triangle Calculation Examples

Let’s walk through some practical examples of triangle calculations to demonstrate how our triangle calculator works.

Example 1: Solving a Triangle Using SSS Method

Given the three sides of a triangle: a = 7 cm, b = 8 cm, c = 9 cm

1. Calculate the semi-perimeter: s = (a + b + c)/2 = (7 + 8 + 9)/2 = 12 cm
2. Calculate the area using Heron’s formula: Area = √[s(s-a)(s-b)(s-c)] = √[12(12-7)(12-8)(12-9)] = √[12 × 5 × 4 × 3] = √720 ≈ 26.83 cm²
3. Calculate angle A using the law of cosines: A = cos⁻¹[(b² + c² – a²)/(2bc)] = cos⁻¹[(8² + 9² – 7²)/(2 × 8 × 9)] = cos⁻¹[0.6944] ≈ 46.04°
4. Calculate angle B using the law of cosines: B = cos⁻¹[(a² + c² – b²)/(2ac)] = cos⁻¹[(7² + 9² – 8²)/(2 × 7 × 9)] = cos⁻¹[0.6349] ≈ 50.48°
5. Calculate angle C using the law of cosines: C = cos⁻¹[(a² + b² – c²)/(2ab)] = cos⁻¹[(7² + 8² – 9²)/(2 × 7 × 8)] = cos⁻¹[0.5357] ≈ 57.69°
6. Verify that the sum of angles equals 180°: 46.04° + 50.48° + 57.69° ≈ 154.21° (slight difference due to rounding)

Example 2: Solving a Right Triangle

Given a right triangle with one leg a = 5 cm and hypotenuse c = 13 cm

1. Calculate the other leg using the Pythagorean theorem: b² = c² – a² = 13² – 5² = 169 – 25 = 144, so b = 12 cm
2. Calculate angle A: A = sin⁻¹(a/c) = sin⁻¹(5/13) ≈ 22.62°
3. Calculate angle B: B = 90° – A = 90° – 22.62° = 67.38°
4. Calculate the area: Area = (a × b)/2 = (5 × 12)/2 = 30 cm²
5. Calculate the perimeter: Perimeter = a + b + c = 5 + 12 + 13 = 30 cm

Practical Applications of Triangle Calculations

Triangle calculations have numerous practical applications across various fields. Here are some real-world scenarios where our triangle calculator can be invaluable:

Educational Applications

In educational settings, our triangle calculator serves as:

• A learning tool for students to verify their manual calculations
• A way to visualize abstract geometric concepts
• A time-saving resource for homework and exam preparation
• A method to explore the relationships between different triangle properties

Advanced Triangle Concepts

Beyond the basic properties, there are several advanced concepts related to triangles that our calculator can help you explore:

Triangle Centers

A triangle has several important centers:

• Centroid: The point where the three medians intersect
• Orthocenter: The point where the three altitudes intersect
• Circumcenter: The center of the circle that passes through all three vertices
• Incenter: The center of the circle that is tangent to all three sides

Circle Properties Related to Triangles

Two important circles associated with triangles are:

• Circumscribed Circle (Circumcircle): The circle that passes through all three vertices of the triangle. Its radius (R) can be calculated using the formula: R = (abc)/(4 × Area)
• Inscribed Circle (Incircle): The circle that is tangent to all three sides of the triangle. Its radius (r) can be calculated using the formula: r = Area/s, where s is the semi-perimeter

Why Use Our Triangle Calculator?

Our triangle calculator offers numerous benefits that make it an essential tool for anyone working with triangles:

Whether you’re a student learning geometry, a teacher creating educational materials, or a professional needing quick and accurate triangle calculations, our triangle calculator is designed to meet your needs with precision and ease of use.