Use our Present Value Calculator to determine the current value of future cash flows. Plan investments and make informed financial decisions with confidence.
Understanding the time value of money is crucial for making informed financial decisions. Our present value calculator helps you determine what a future sum of money is worth in today’s dollars. Whether you’re evaluating an investment opportunity, planning for retirement, or analyzing loan options, this tool provides the insights you need to make sound financial choices.
Calculate Present Value Now
Find out what your future money is worth today with our easy-to-use calculator.
What Is Present Value?

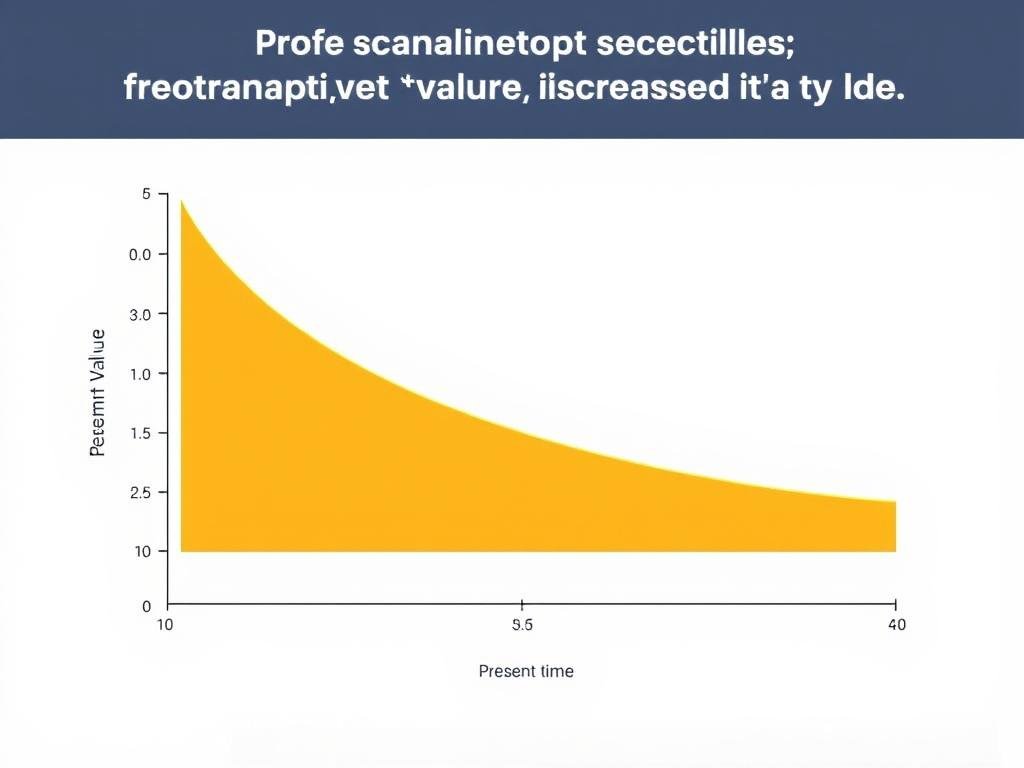
Present value shows how future money is worth less today due to time value of money
Present value (PV) is a financial concept that determines the current worth of a future sum of money or stream of cash flows given a specified rate of return. In other words, it answers the question: “What is the value today of money I’ll receive in the future?”
The concept is based on the time value of money principle, which states that a dollar today is worth more than a dollar in the future because of its potential earning capacity. Money available now can be invested to earn interest and grow over time.
For example, if you’re promised $10,000 in five years, that amount is worth less than $10,000 today. The present value calculation tells you exactly how much less, based on the potential interest rate you could earn if you had the money now.
Present value is one of the most fundamental concepts in finance, used to price everything from bonds and stocks to real estate investments and business valuations.
Present Value Formula
The basic present value formula is straightforward but powerful. To calculate the present value of a future sum, you divide the future value by (1 + interest rate) raised to the power of the number of periods.
PV = FV / (1 + r)^n
Where:
- PV = Present value
- FV = Future value
- r = Interest rate (as a decimal)
- n = Number of periods (typically years)
This formula applies compound interest, which means that interest increases exponentially over subsequent periods. The higher the interest rate or the longer the time period, the lower the present value will be.
How to Calculate Present Value
Calculating present value involves a few simple steps:
- Determine the future value (FV) – the amount you expect to receive in the future
- Identify the interest rate (r) – the rate of return you could earn on an investment
- Specify the number of periods (n) – typically in years
- Apply the present value formula: PV = FV / (1 + r)^n
Example Calculation
Let’s work through a simple example to illustrate how present value works:
Example: What is the present value of $5,000 to be received in 3 years if the interest rate is 6%?
Using the formula: PV = FV / (1 + r)^n
PV = $5,000 / (1 + 0.06)^3
PV = $5,000 / 1.191
PV = $4,198.15
This means that $4,198.15 today is equivalent to $5,000 in 3 years, assuming a 6% interest rate.
Try Your Own Calculation
Use our calculator to find the present value of your future money without doing the math manually.
Real-World Applications of Present Value
Present value calculations are used in numerous financial scenarios:
Investment Analysis

Investors use present value to determine if the future returns of an investment justify the initial cost. By calculating the present value of expected cash flows, they can make informed decisions about whether to invest.
Retirement Planning

When planning for retirement, present value helps determine how much you need to save now to achieve your desired retirement income. It accounts for the effects of inflation and investment returns.
Loan Analysis

Lenders use present value to determine loan amounts and interest rates. Borrowers can use it to compare different loan offers and understand the true cost of borrowing.
Understanding present value gives you the power to compare financial options that involve different amounts of money at different points in time.
Present Value vs. Future Value
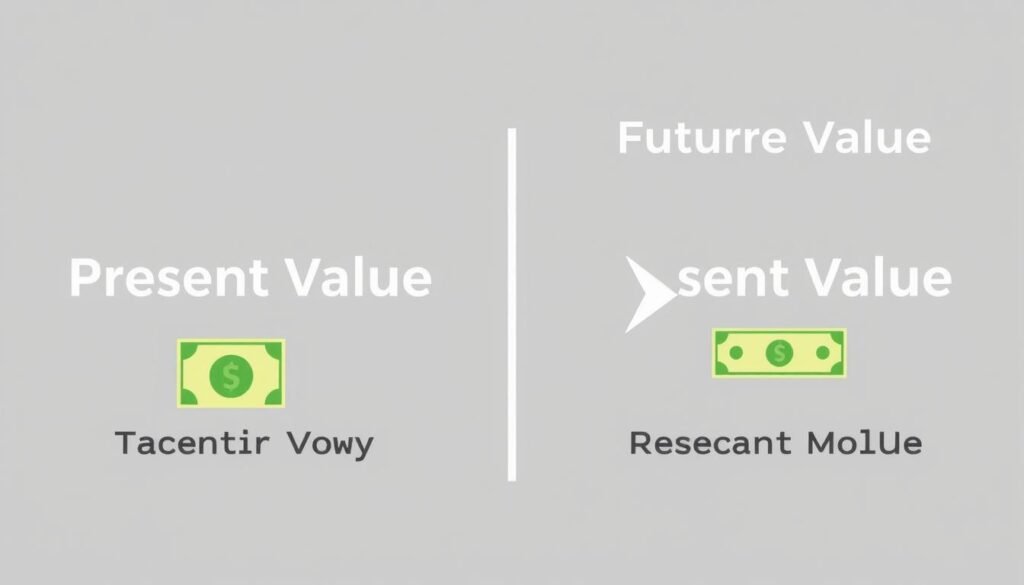
Present Value
- Determines what future money is worth today
- Discounts future amounts back to the present
- Used to evaluate investments and compare options
- Formula: PV = FV / (1 + r)^n
Future Value
- Calculates what present money will be worth in the future
- Compounds present amounts forward in time
- Used for savings goals and growth projections
- Formula: FV = PV × (1 + r)^n
While present value and future value are opposite concepts, they’re two sides of the same coin. Understanding both gives you a complete picture of how money changes value over time.
| Aspect | Present Value | Future Value |
| Direction | Backward-looking (future to present) | Forward-looking (present to future) |
| Effect of Time | Decreases with longer time periods | Increases with longer time periods |
| Effect of Interest Rate | Higher rates decrease present value | Higher rates increase future value |
| Primary Use | Investment analysis, comparing options | Savings goals, growth projections |
Advanced Present Value Concepts
Present Value of Annuities
An annuity is a series of equal payments made at regular intervals. The present value of an annuity calculates what these future payment streams are worth today.
PV of Ordinary Annuity = PMT × [1 – (1 + r)^-n] / r
Where:
- PMT = Payment amount per period
- r = Interest rate per period
- n = Number of periods

Present Value of Perpetuities
A perpetuity is an annuity that continues indefinitely. The present value of a perpetuity is calculated using a simplified formula:
PV of Perpetuity = PMT / r
Where:
- PMT = Payment amount per period
- r = Interest rate per period
Present Value with Varying Cash Flows
When cash flows vary over time, you need to calculate the present value of each payment separately and then sum them:
PV = CF₁/(1+r)¹ + CF₂/(1+r)² + CF₃/(1+r)³ + … + CFₙ/(1+r)ⁿ
Where:
- CF₁, CF₂, etc. = Cash flow in period 1, 2, etc.
- r = Interest rate per period
- n = Number of periods
Handle Complex Calculations Easily
Our calculator can handle various present value scenarios, including annuities and varying cash flows.
Common Mistakes When Calculating Present Value

Best Practices
- Use consistent time periods for all variables
- Convert annual rates to match the period frequency
- Account for inflation when appropriate
- Use realistic interest/discount rates
- Double-check your calculations with a reliable calculator
Common Errors
- Using inconsistent time periods
- Forgetting to convert interest rates to decimals
- Ignoring inflation in long-term calculations
- Using unrealistic discount rates
- Confusing present value with future value formulas
Important: When calculating present value, even small errors in the interest rate or time period can lead to significant differences in the result, especially for calculations spanning many years.
Practical Examples of Present Value Calculations
Example 1: Investment Decision
Scenario: You’re considering an investment that promises to pay $20,000 after 5 years. If you require a 7% annual return on your investments, should you pay $15,000 for this opportunity?
Calculation:
PV = $20,000 / (1 + 0.07)^5
PV = $20,000 / 1.4026
PV = $14,259.52
Decision: Since the present value ($14,259.52) is less than the asking price ($15,000), this investment doesn’t meet your 7% return requirement. You should either negotiate a lower price or look for alternative investments.
Example 2: Retirement Planning
Scenario: You want to have $500,000 for retirement in 25 years. Assuming an average annual return of 6%, how much do you need to invest as a lump sum today?
Calculation:
PV = $500,000 / (1 + 0.06)^25
PV = $500,000 / 4.2919
PV = $116,498.99
Decision: You need to invest approximately $116,499 today as a lump sum to reach your retirement goal of $500,000 in 25 years, assuming a 6% annual return.

Example 3: Loan Comparison
Scenario: You’re comparing two loan offers:
- Loan A: $10,000 now at 5% interest for 3 years
- Loan B: $9,500 now with a balloon payment of $12,000 after 3 years
Calculation for Loan A:
Total repayment = $10,000 × (1 + 0.05)^3 = $11,576.25
Calculation for Loan B:
$12,000 balloon payment
Comparison:
Loan A costs $11,576.25 – $10,000 = $1,576.25 in interest
Loan B costs $12,000 – $9,500 = $2,500 in interest
Decision: Loan A has a lower total interest cost and would be the better choice.
Present Value Calculator
Use our free calculator to determine the present value of your future money. Simply enter the future amount, interest rate, and time period to get your result instantly.
Frequently Asked Questions About Present Value
Why is present value important in financial decision-making?
Present value is crucial because it allows you to compare financial options that involve different amounts of money at different points in time. It accounts for the time value of money, recognizing that money available today is worth more than the same amount in the future due to its potential earning capacity. This concept helps in making informed investment decisions, evaluating loan options, planning for retirement, and many other financial scenarios.
How does inflation affect present value calculations?
Inflation decreases the purchasing power of money over time. In present value calculations, inflation can be accounted for by adjusting the discount rate. If you’re using a nominal interest rate (not adjusted for inflation), the resulting present value will be in nominal terms. For a more accurate representation of purchasing power, you can use a real interest rate (nominal rate minus inflation rate) in your calculations.
What’s the difference between simple and compound interest in present value?
The standard present value formula assumes compound interest, where interest is earned on both the principal and previously accumulated interest. With simple interest, interest is only earned on the principal amount. Most financial calculations use compound interest because it more accurately reflects how money grows in real-world financial products. The difference becomes more significant over longer time periods.
How do I determine the appropriate discount rate for present value calculations?
The appropriate discount rate depends on the context of your calculation:
- For personal financial decisions, you might use the rate of return you could earn on alternative investments with similar risk.
- For business decisions, companies often use their weighted average cost of capital (WACC).
- For adjusting for inflation only, you would use the expected inflation rate.
- For risk-adjusted calculations, higher discount rates are used for riskier cash flows.
The discount rate should reflect opportunity cost, risk, and time preference.
Can present value be negative?
Present value itself is typically positive when calculating the worth of future positive cash flows. However, in net present value (NPV) calculations, which include both inflows and outflows, the result can be negative. A negative NPV suggests that an investment would not meet the required rate of return and might not be financially viable.
Conclusion
Understanding present value is essential for making informed financial decisions. By determining what future money is worth today, you can evaluate investments, plan for retirement, analyze loans, and compare financial options on an equal footing.
Our present value calculator simplifies these complex calculations, allowing you to quickly and accurately determine present values without the need for manual calculations or financial expertise.
Remember that the time value of money is a fundamental concept in finance, and mastering present value calculations gives you a powerful tool for managing your financial future.
Start Making Better Financial Decisions Today
Use our free Present Value Calculator to evaluate your financial options and make informed decisions based on the time value of money.